题目内容
4.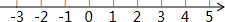 解不等式组$\left\{\begin{array}{l}{x-2≤1}\\{2x+3≥1}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{x-2≤1}\\{2x+3≥1}\end{array}\right.$,并把解集在数轴上表示出来.
分析 首先根据解一元一次不等式组的方法,求出不等式组$\left\{\begin{array}{l}{x-2≤1}\\{2x+3≥1}\end{array}\right.$中每个不等式的解集;然后找出每个不等式的解集的公共部分,求出不等式组$\left\{\begin{array}{l}{x-2≤1}\\{2x+3≥1}\end{array}\right.$的解集;最后把不等式组的解集在数轴上表示出来即可.
解答 解:∵$\left\{\begin{array}{l}{x-2≤1}\\{2x+3≥1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x≤3}\\{x≥-1}\end{array}\right.$
∴-1≤x≤3,
把不等式组$\left\{\begin{array}{l}{x-2≤1}\\{2x+3≥1}\end{array}\right.$的解集在数轴上表示出来为: .
.
点评 (1)此题主要考查了解一元一次不等式组问题,要熟练掌握,解答此题的关键是要明确一元一次不等式组的解法以及解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
(2)此题还考查了在数轴上表示不等式的解集的方法,要熟练掌握,解答此题的关键是要明确:用数轴表示不等式的解集时,要注意“两定”:一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;二是定方向,定方向的原则是:“小于向左,大于向右”.

练习册系列答案
相关题目
9.下列事件属于不可能事件的是( )
| A. | 明天下雨 | |
| B. | 小李坐车过十字路口,全是绿色指示灯 | |
| C. | 3人分成两组,每组只有一人 | |
| D. | 射击时,靶中10环 |
14.对于函数y=$\frac{4}{x}$,下列说法错误的是( )
| A. | 这个函数的图象位于第一、第三象限 | |
| B. | 这个函数的图象既是轴对称图形又是中心对称图形 | |
| C. | 当x>0时,y随x的增大而增大 | |
| D. | 当x<0时,y随x的增大而减小 |