题目内容
14.在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2向右平移8个单位得到直线m,那么直线m与y轴的交点坐标是(0,-2).分析 直接根据“左加右减”的原则进行解答,再把x=0代入所得的解析式解答即可.
解答 解:直线y=$\frac{1}{2}$x+2向右平移8个单位得到直线m,
可得直线m的解析式为:y=$\frac{1}{2}$(x-8)+2=$\frac{1}{2}$x-2,
把x=0代入y=$\frac{1}{2}$x-2=-2,
所以直线m与y轴的交点坐标是(0,-2),
故答案为:(0,-2).
点评 本题考查的是一次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
2.已知方程4x2-(2m+3)x+10=0的一个根为-2,则m的值为( )
| A. | 8 | B. | -8 | C. | -$\frac{5}{4}$ | D. | $\frac{4}{5}$ |
9.下列各数:3.14159,-$\root{3}{8}$,0.3131131113…(相邻两个3之间1的个数逐次加1),-π,$\sqrt{256}$,-$\frac{1}{7}$.其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.今年马铃薯喜获丰收,某生产基地收获马铃薯40吨.经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨马铃薯的利润如表:
设按计划全部销售出后的总利润为y元,其中排放量为x吨,且加工销售量为15吨.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完马铃薯后获得的最大利润.
| 销售方式 | 批发 | 零售 | 加工销售 |
| 利润(元/吨) | 1200 | 2200 | 3000 |
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完马铃薯后获得的最大利润.

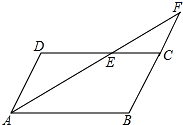 如图,平行四边形ABCD中,AB=5,AD=2,AE平分∠DAB交DC于E点,交BC的延长线于F点,则CF=3.
如图,平行四边形ABCD中,AB=5,AD=2,AE平分∠DAB交DC于E点,交BC的延长线于F点,则CF=3. 如图,在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8cm,r=1.6
如图,在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8cm,r=1.6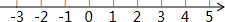 解不等式组$\left\{\begin{array}{l}{x-2≤1}\\{2x+3≥1}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{x-2≤1}\\{2x+3≥1}\end{array}\right.$,并把解集在数轴上表示出来.