题目内容
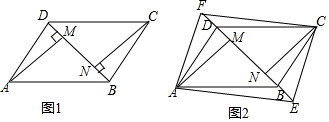
7.如图(1),四边形ABCD是平行四边形,BD是它的一条对角线,过顶点A、C分别作AM⊥BD,CN⊥BD,M,N为垂足.(1)求证:AM=CN;
(2)如图(2),在对角线DB的延长线及反向延长线上分别取点E,F,使BE=DF,连接AE、CF,试探究:当EF满足什么条件时,四边形AECF是矩形?并加以证明.
分析 (1)利用平行四边形的性质证得△AMD≌△CNB,从而根据全等三角形对应边相等证得结论即可;
(2)利用对角线相等的平行四边形是矩形证得结论即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠ADM=∠CBN.
∵AM⊥BD,CN⊥BD,
∴∠AMD=∠CNB=90°,
在△AMD和△CNB中$\left\{\begin{array}{l}{∠ADM=∠CEN}\\{∠AMD=∠CNB}\\{AD=BC}\end{array}\right.$,
∴△AMD≌△CNB.
∴AM=CN.
(2)猜想:当EF=AC时,四边形AECF是矩形.
证明:由(1)得△AMD≌△CNB,
∴DM=BN.
∵BE=DF,
∴DM+DF=BN+BE,即MF=NE.
在△AMF和△CNE中$\left\{\begin{array}{l}{MF=NE}\\{∠AMF=∠CNE}\\{AM=CN}\end{array}\right.$
∴△AMF≌△CNE.
∴AF=CE,∠AFE=∠CEF.
∴AF∥CE且AF=CE.
即四边形AECF是平行四边形.
又EF=AC,
∴四边形AMCN是矩形.
点评 本题考查了平行四边形对边平行且相等的性质,平行线的性质,全等三角形的判定与性质,是基础题,一般情况下,证明边相等,就利用边所在的三角形全等证明.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


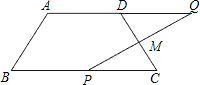 如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.