题目内容
17．（1）2sin30°+$\sqrt{3}$tan60°-$\sqrt{2}$cos45°（2）若$\frac{x}{y}$=$\frac{1}{3}$，求$\frac{2x+y}{x-y}$的值．
分析 （1）将特殊角的三角函数值代入，再根据实数的运算法则计算即可；
（2）由$\frac{x}{y}$=$\frac{1}{3}$，可得y=3x，代入$\frac{2x+y}{x-y}$，计算即可．
解答 解：（1）2sin30°+$\sqrt{3}$tan60°-$\sqrt{2}$cos45°
=2×$\frac{1}{2}$+$\sqrt{3}$×$\sqrt{3}$-$\sqrt{2}$×$\frac{\sqrt{2}}{2}$
=1+3-1
=3；
（2）∵$\frac{x}{y}$=$\frac{1}{3}$，
∴y=3x，
∴$\frac{2x+y}{x-y}$=$\frac{2x+3x}{x-3x}$=-$\frac{5}{2}$．
点评 本题考查了比例的基本性质，实数的运算，以及特殊角的三角函数值，比较简单．
练习册系列答案
相关题目
7．若a=2016，b=-2017，则分式1+$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$÷$\frac{1}{a}$的值是（ ）
| A． | 2016 | B． | 0 | C． | -2017 | D． | 4034 |
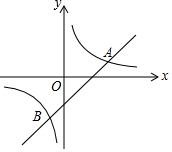如图，直线y=x-2与反比例函数y=$\frac{k}{x}$的图象交于点A（3，1）和点B．
如图，在平面直角坐标系中，点P从原点O出发．沿x轴向右以每秒一个单位长的速度运动t秒（t＞0），抛物线y=-x2+bx+c经过点O和点P．
