题目内容
6. 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米.(1)请以AB所在直线为x轴(射线AB的方向为正方向),线段AB的垂直平分线为y轴建立平面直角坐标系,求出抛物线的解析式;
(2)若要搭建一个矩形“支架CD-DE-EF,使D、E两点在抛物线上,C、F两点在地面AB上,若AC=2米,求支架的总长度.
分析 (1)根据题意可以画出相应的平面直角坐标系,然后根据平面直角坐标系可以写出顶点的坐标和点A相应的点的坐标,然后设出二次函数的顶点式,即可求得二次函数的解析式;
(2)根据题意可知点C的坐标,从而可以得到点D的横坐标,然后代入二次函数解析式即可求得点D的纵坐标,从而可以求得CD、DE、EF的长,从而可以求得支架的总长度.
解答 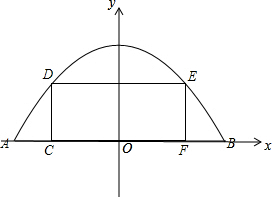 解:(1)AB所在直线为x轴(射线AB的方向为正方向),线段AB的垂直平分线为y轴建立平面直角坐标系如右图所示,
解:(1)AB所在直线为x轴(射线AB的方向为正方向),线段AB的垂直平分线为y轴建立平面直角坐标系如右图所示,
∵由题意和图象可知,该抛物线过点(-6,0),顶点坐标是(0,6),
∴抛物线的解析式为:y=ax2+6,
∴0=a×(-6)2+6,
解得,a=$-\frac{1}{6}$,
即$y=-\frac{1}{6}{x}^{2}$+6;
(2)∵AC=2,
∴点C的坐标是(-4,0),
∴点D的横坐标是-4,
将x=-4代入$y=-\frac{1}{6}{x}^{2}$+6得,y=$\frac{10}{3}$,
∴CD=EF=$\frac{10}{3}$,DE=4-(-4)=8,
∴CD+DE+EF=$\frac{10}{3}+8+\frac{10}{3}=14\frac{2}{3}$,
即支架的总长度是$14\frac{2}{3}$米.
点评 本题考查二次函数的应用,解题的关键是明确题意,画出相应的平面直角坐标系,求出各点对应的坐标,利用数形结合的思想解答问题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18.在平面直角坐标系中,点(-1,2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.函数y=$\frac{k}{x}$的图象经过点(2,3),则k=( )
| A. | 2 | B. | 3 | C. | 6 | D. | -6 |
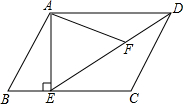 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.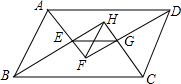 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.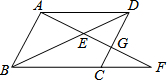 如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$.
如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$. 如图是由六个相同的小正方体组成的立方体图形,它的俯视图是( )
如图是由六个相同的小正方体组成的立方体图形,它的俯视图是( )


