题目内容
 ①一圆锥的底面半径为6cm,高为8cm,那么这个圆锥的侧面积是
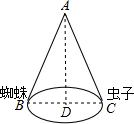
①一圆锥的底面半径为6cm,高为8cm,那么这个圆锥的侧面积是②一圆锥底圆直径BC为24dm,高AD为24
| 2 |
考点:平面展开-最短路径问题,圆锥的计算
专题:
分析:①首先利用勾股定理得出母线长,再利用圆锥侧面积公式求出即可;
②首先利用勾股定理得出母线长,再求出展开图圆心角的度数,即可得出蜘蛛经过锥面路线的最短距离.
②首先利用勾股定理得出母线长,再求出展开图圆心角的度数,即可得出蜘蛛经过锥面路线的最短距离.
解答: 解:①∵一圆锥的底面半径为6cm,高为8cm,
解:①∵一圆锥的底面半径为6cm,高为8cm,
∴圆锥的母线为:10cm,
∴这个圆锥的侧面积是:πrl=π×6×10=60π(cm2),故答案为:60π;
②∵一圆锥底圆直径BC为24dm,高AD为24
dm,
∴圆锥的母线为:
=36(dm),
则2π×12=
,
解得:n=120,
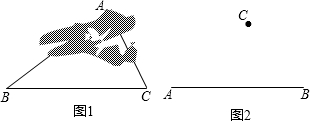
如图所示:过点A作AE⊥BC于点E,
∵∠BAC=120°,
∴∠ABE=30°,
∴BE=AEcos30°=36×
=18
(dm),
故蜘蛛经过锥面路线的最短距离为18
dm.
故答案为:18
dm.
 解:①∵一圆锥的底面半径为6cm,高为8cm,
解:①∵一圆锥的底面半径为6cm,高为8cm,∴圆锥的母线为:10cm,
∴这个圆锥的侧面积是:πrl=π×6×10=60π(cm2),故答案为:60π;
②∵一圆锥底圆直径BC为24dm,高AD为24
| 2 |
∴圆锥的母线为:
122+(24
|
则2π×12=
| nπ×36 |
| 180 |
解得:n=120,
如图所示:过点A作AE⊥BC于点E,
∵∠BAC=120°,
∴∠ABE=30°,
∴BE=AEcos30°=36×
| ||
| 2 |
| 3 |
故蜘蛛经过锥面路线的最短距离为18
| 3 |
故答案为:18
| 3 |
点评:此题主要考查了平面展开图的最短路径问题,利用圆锥侧面展开图得出其母线长是解题关键.

练习册系列答案
相关题目
分式方程
-1=
的解是( )
| x |
| x-1 |
| 3 |
| (x-1)(x+2) |
| A、x=1 | ||
B、x=-1+
| ||
| C、x=2 | ||
| D、无解 |
 如图所示是某种机器活塞的三视图,请根据三视图写出该活塞的几何体名称,并计算其体积.
如图所示是某种机器活塞的三视图,请根据三视图写出该活塞的几何体名称,并计算其体积. 如图,在平面直角坐标系内,半径为t的圆D与x轴交于点A(1,0),B(5,0),点D在第一象限,点C的坐标为(0,-2).
如图,在平面直角坐标系内,半径为t的圆D与x轴交于点A(1,0),B(5,0),点D在第一象限,点C的坐标为(0,-2). 已知:如图,在△ABC中,BP、CP分别平分∠ABC和∠ACB,DE过点P交AB于D,交AC于E,且DE∥BC.求证:DE=EC+DB.
已知:如图,在△ABC中,BP、CP分别平分∠ABC和∠ACB,DE过点P交AB于D,交AC于E,且DE∥BC.求证:DE=EC+DB.