题目内容
关于x的一元二次方程ax2+bx+c=3(a≠0)的一个根为x=2,且二次函数y=ax2+bx+c的图象的对称轴是直线x=2,则该图象的顶点坐标为 .
考点:抛物线与x轴的交点
专题:
分析:由于方程ax2+bx+c=3的一个根为x=2,代入得到一个式子,然后再根据二次函数y=ax2+bx+c的对称轴是直线x=2,得y=4a+2b+c=3,从而得到抛物线的顶点坐标.
解答:解:∵关于x的一元二次方程ax2+bx+c=3的一个根为x=2,
∴4a+2b+c=3,
∵二次函数y=ax2+bx+c的对称轴是直线x=2,
∴顶点的横坐标为2,
将x=2代入二次函数解析式得:y=4a+2b+c
∴y=3,
∴函数的顶点坐标为:(2,3).
故答案为(2,3).
∴4a+2b+c=3,
∵二次函数y=ax2+bx+c的对称轴是直线x=2,
∴顶点的横坐标为2,
将x=2代入二次函数解析式得:y=4a+2b+c
∴y=3,
∴函数的顶点坐标为:(2,3).
故答案为(2,3).
点评:此题主要考查了一元二次方程与函数的关系,函数与x轴的交点的横坐标就是方程的根,若方程无根说明函数与x轴无交点,另外还考查的函数的对称轴及顶点坐标.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
下列运算正确是( )
A、6
| ||||||
B、a2
| ||||||
C、-2
| ||||||
D、
|
一个正偶数的算术平方根是a,那么与这个正偶数相邻的下一个正偶数的算术平方根是( )
| A、a+2 | ||
| B、a2+2 | ||
C、
| ||
D、
|
下列命题是假命题的是( )
| A、如果两个角是对顶角,那么它们相等 |
| B、同位角相等 |
| C、三角形中相等的边所对的角相等 |
| D、全等直角三角形的两锐角对应相等 |
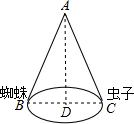 ①一圆锥的底面半径为6cm,高为8cm,那么这个圆锥的侧面积是
①一圆锥的底面半径为6cm,高为8cm,那么这个圆锥的侧面积是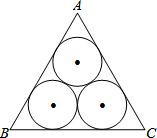 如图,三个半径都为6cm的等圆两两外切,并且△ABC的每一边都与其中两个圆相切,则△ABC的周长为
如图,三个半径都为6cm的等圆两两外切,并且△ABC的每一边都与其中两个圆相切,则△ABC的周长为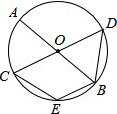 已知AB、CD是⊙O的两条直径,CE∥AB,求证:
已知AB、CD是⊙O的两条直径,CE∥AB,求证: