题目内容
 如图,在平面直角坐标系内,半径为t的圆D与x轴交于点A(1,0),B(5,0),点D在第一象限,点C的坐标为(0,-2).
如图,在平面直角坐标系内,半径为t的圆D与x轴交于点A(1,0),B(5,0),点D在第一象限,点C的坐标为(0,-2).(1)当t为何值时,圆D与y轴相切,并求出圆心D的坐标;
(2)直接写出当t为何值时,圆D与y轴相交,相离.
考点:直线与圆的位置关系,坐标与图形性质
专题:
分析:(1)根据垂径定理求出AE和BE,求出OE,根据勾股定理求出DE,即可得出答案;
(2)根据直线与圆的位置关系得出即可.
(2)根据直线与圆的位置关系得出即可.
解答:解:(1)∵DE⊥AB,DE过D,A(1,0),B(5,0),
∴AE=BE=
(5-1)=2,
∴OE=1+2=3,
即当半径t=3时,圆D与y轴相切,
在Rt△DEA中,AD=3,AE=2,由勾股定理得:DE=
=
,
即圆心D的坐标是(3,
);
(2)当2<t<3时,圆D与y轴相离,当t>3时,圆D与y轴相交.
∴AE=BE=
| 1 |
| 2 |
∴OE=1+2=3,
即当半径t=3时,圆D与y轴相切,
在Rt△DEA中,AD=3,AE=2,由勾股定理得:DE=
| 32-22 |
| 5 |
即圆心D的坐标是(3,
| 5 |
(2)当2<t<3时,圆D与y轴相离,当t>3时,圆D与y轴相交.
点评:本题考查了勾股定理,垂径定理,直线与圆的位置关系的应用,注意:直线与圆的位置关系有相离,相交,相切.

练习册系列答案
相关题目
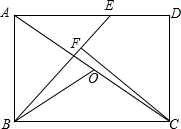 如图,在矩形ABCD中,点E是AD上一点,连接BE,且BE=BC,∠EBC=45°,CF⊥BE于点F,O为AC的中点,AB=2.
如图,在矩形ABCD中,点E是AD上一点,连接BE,且BE=BC,∠EBC=45°,CF⊥BE于点F,O为AC的中点,AB=2.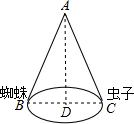 ①一圆锥的底面半径为6cm,高为8cm,那么这个圆锥的侧面积是
①一圆锥的底面半径为6cm,高为8cm,那么这个圆锥的侧面积是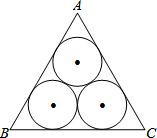 如图,三个半径都为6cm的等圆两两外切,并且△ABC的每一边都与其中两个圆相切,则△ABC的周长为
如图,三个半径都为6cm的等圆两两外切,并且△ABC的每一边都与其中两个圆相切,则△ABC的周长为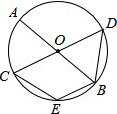 已知AB、CD是⊙O的两条直径,CE∥AB,求证:
已知AB、CD是⊙O的两条直径,CE∥AB,求证:
 如图,在△ABC中,DE∥BC,交AB于D,交AC于E,F为BC上的一点,DE交AF于G,AD=2BD,AE=5,求:
如图,在△ABC中,DE∥BC,交AB于D,交AC于E,F为BC上的一点,DE交AF于G,AD=2BD,AE=5,求: