题目内容
16.阅读下列材料:(1)∵$\frac{1}{1×3}$=$\frac{1}{2}(1-\frac{1}{3})$ $\frac{1}{3×5}$=$\frac{1}{2}(\frac{1}{3}-\frac{1}{5})$ $\frac{1}{5×7}$=$\frac{1}{2}(\frac{1}{5}-\frac{1}{7})$…$\frac{1}{17×19}$=$\frac{1}{2}(\frac{1}{17}-\frac{1}{19})$
∴$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{17×19}$
=$\frac{1}{2}(1-\frac{1}{3})$+$\frac{1}{2}(\frac{1}{3}-\frac{1}{5})$+$\frac{1}{2}(\frac{1}{5}-\frac{1}{7})$+…+$\frac{1}{2}(\frac{1}{17}-\frac{1}{19})$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{17}$-$\frac{1}{19}$)=$\frac{1}{2}(1-\frac{1}{19})$=$\frac{9}{19}$
问题:通过阅读,你一定学会了一种解决问题的方法,请你用学到的方法计算:
$\frac{1}{x(x+3)}$+$\frac{1}{(x+3)(x+6)}$+…+$\frac{1}{(x+15)(x+18)}$.
分析 根据阅读材料把每个部分分成两个式子的差的形式,即可化简求解.
解答 解:原式=$\frac{1}{3}$($\frac{1}{x}$-$\frac{1}{x+3}$+$\frac{1}{x+3}$-$\frac{1}{x+6}$+…+$\frac{1}{x+15}$-$\frac{1}{x+18}$)=$\frac{1}{3}$($\frac{1}{x}$-$\frac{1}{x+18}$)=$\frac{1}{3}$×$\frac{18}{x(x+18)}$=$\frac{6}{x(x+18)}$.
点评 本题考查了分式的化简求值,正确读懂阅读材料是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知A($\sqrt{2}$,1)是正比例函数图象上一点,此函数图形与x轴正半轴夹角α的cosα的值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
6.已知a=$\sqrt{2}$,b=$\sqrt{5}$,则$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}÷\frac{1}{a}$的值为( )
| A. | $\sqrt{5}-\sqrt{2}$ | B. | 3 | C. | $\sqrt{2}+\sqrt{5}$ | D. | $\sqrt{2}-\sqrt{5}$ |
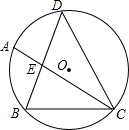 如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E,
如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E,