题目内容
7.△ABC的边BC=$\sqrt{2}$cm,其外接圆的半径为1cm,那么∠A=45°.分析 连接OB,作OH⊥BC于H,根据垂径定理求出BH的长,根据正弦的概念求出∠BOH的度数,根据圆周角定理得到答案.
解答  解:连接OB,作OH⊥BC于H,
解:连接OB,作OH⊥BC于H,
则BH=$\frac{1}{2}$BC=$\frac{\sqrt{2}}{2}$,又OB=1,
∴sin∠BOH=$\frac{BH}{OB}$=$\frac{\sqrt{2}}{2}$,
∴∠BOH=45°,
∴∠A=45°,
故答案为:45°.
点评 本题考查的是三角形的外接圆与外心的知识,掌握垂径定理、锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
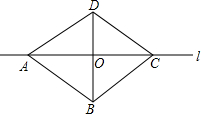 如图所示,直线l是四边形ABCD的对称轴,若AB=CD,有下面4个结论:
如图所示,直线l是四边形ABCD的对称轴,若AB=CD,有下面4个结论: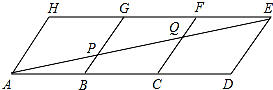 如图,用三个全等的平行四边形ABGH,BCFG,CDEF拼成平行四边形ADEH,连结AE与BG,CF分别交于点P、Q.
如图,用三个全等的平行四边形ABGH,BCFG,CDEF拼成平行四边形ADEH,连结AE与BG,CF分别交于点P、Q.