题目内容
8.已知直线y=$\frac{1}{2}$x+k-2,不经过第二象限,求k的取值范围.分析 由直线y=$\frac{1}{2}$x+k-2不经过第二象限,可得直线y=$\frac{1}{2}$x+k-2经过第一、三象限或第一、三、四象限,根据一次函数图象与系数的关系即可求出k的取值范围.
解答 解:∵直线y=$\frac{1}{2}$x+k-2不经过第二象限,
∴当经过第一、三象限时,k-2=0,可得:k=2.
当经过第一、三、四象限时,k-2<0,可得:k<2
∴k≤2.
点评 本题考查了一次函数y=kx+b(k≠0,k,b为常数)图象与系数的关系:
①k>0,b>0?y=kx+b的图象在一、二、三象限;
②k>0,b<0?y=kx+b的图象在一、三、四象限;
③k<0,b>0?y=kx+b的图象在一、二、四象限;
④k<0,b<0?y=kx+b的图象在二、三、四象限.
⑤k>0,b=0?y=kx+b的图象在一、三象限;
⑥k<0,b=0?y=kx+b的图象在二、四象限.

练习册系列答案
相关题目
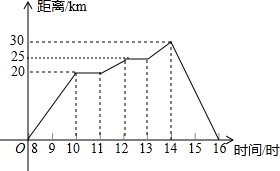 假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示. 如图,有一幅长方形山水画,它的长为90cm,宽为50cm,现在需要它的四周加装一个木框,由于悬挂位置的限制,装上后整体周长不能超过320cm,那么加装的木框条的最大宽度是多少?
如图,有一幅长方形山水画,它的长为90cm,宽为50cm,现在需要它的四周加装一个木框,由于悬挂位置的限制,装上后整体周长不能超过320cm,那么加装的木框条的最大宽度是多少?