题目内容
19.若关于x的不等式组$\left\{\begin{array}{l}{\frac{x}{2}+\frac{x+1}{3}>0}\\{3a+5a+4>4(x+1)+3a}\end{array}\right.$恰有三个整数解,化简:|a-1|+|a-$\frac{3}{2}$|.分析 先求出每个不等式的解集,再根据不等式组的解集得出a的范围,最后化简绝对值即可.
解答 解:$\left\{\begin{array}{l}{\frac{x}{2}+\frac{x+1}{3}>0①}\\{3a+5a+4>4(x+1)+3a②}\end{array}\right.$,
∵解不等式①得:x$>-\frac{2}{5}$,
解不等式②得:x<$\frac{5a}{4}$,
∴不等式组的解集为-$\frac{2}{5}$<x<$\frac{5a}{4}$,
∵有三个整数解,
所以可得:$2<\frac{5a}{4}≤3$,
解得:$\frac{8}{5}<a≤\frac{12}{5}$,
所以|a-1|+|a-$\frac{3}{2}$|=a-1+$\frac{3}{2}-a$=$\frac{1}{2}$.
点评 本题考查了解一元一次不等式组,不等式组的整数解的应用,解此题的关键是能求出不等式组的解集.

练习册系列答案
相关题目
10.计算(+7)-(+5)-(-9)+(-4)时,首先应把它化简,下列化简结果正确的是( )
| A. | -7-5+9-4 | B. | 7-5+9-4 | C. | 7-5-9-4 | D. | 7+5+9-4 |
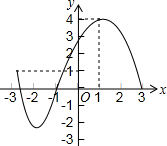 已知某一函数的图象如图所示,根据图象回答下列问题:
已知某一函数的图象如图所示,根据图象回答下列问题: 如图所示,一架云梯AB斜靠在一面墙上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿底面向右滑行.
如图所示,一架云梯AB斜靠在一面墙上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿底面向右滑行.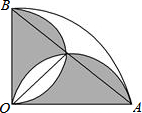 半径1cm,圆心角90度的扇形OAB中,分别以OA,OB为直径作半圆,则阴影部分(两个半圆除了重叠部分其余部分)面积为$\frac{1}{2}$.
半径1cm,圆心角90度的扇形OAB中,分别以OA,OB为直径作半圆,则阴影部分(两个半圆除了重叠部分其余部分)面积为$\frac{1}{2}$.