题目内容
等腰△ABC中,AB=AC,边AB绕点A逆时针旋转角度m得到线段AD.
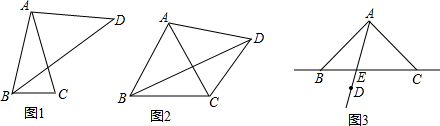
(1)如图1,若∠BAC=30°,30°<m<180°,连接BD,请用含m的式子表示∠DBC的度数;
(2)如图2,若∠BAC=60°,0°<m<360°,连接BD,DC,直接写出△BDC为等腰三角形时m所有可能的取值 ;
(3)如图3,若∠BAC=90°,射线AD与直线BC相交于点E,是否存在旋转角度m,使
=
?若存在,求出所有符合条件的m的值;若不存在,请说明理由.

(1)如图1,若∠BAC=30°,30°<m<180°,连接BD,请用含m的式子表示∠DBC的度数;
(2)如图2,若∠BAC=60°,0°<m<360°,连接BD,DC,直接写出△BDC为等腰三角形时m所有可能的取值
(3)如图3,若∠BAC=90°,射线AD与直线BC相交于点E,是否存在旋转角度m,使
| AE |
| BE |
| 2 |
考点:旋转的性质,等腰三角形的性质
专题:
分析:(1)根据三角形内角和和等腰三角形的性质分别求出∠ABC,∠ABD的度数,相减即可求解;
(2)分四种情况讨论得到△BDC为等腰三角形时m的取值即可;
(3)分E点在BC上和CB的延长线上两种情况讨论求解.
(2)分四种情况讨论得到△BDC为等腰三角形时m的取值即可;
(3)分E点在BC上和CB的延长线上两种情况讨论求解.
解答:解:(1)∠ABC=(180°-30°)÷2=75°,
∠ABD=(180°-m)÷2=90°-
m,
∠DBC=∠ABC-∠ABD=75°-(90°-
m)=
m-15°;

(2)由分析图形可知m的取值为:
30°,120°,210°,300°,
故答案为:30°,120°,210°,300°;
(3)存在2个符合条件的m的值:m=30°或m=330°.
如图①:过E作EF⊥AB于F.
在Rt△BEF中,∵∠FBE=45°,
∴BE=
EF,
∵AE:BE=
;
∴AE=2EF;
又∵∠AFE=90°;
∴∠FAE=30°.即m=30°
在Rt△AEF中,∵∠FAE=30°,
∴AE=2EF,
∴AE:BE=
;
如图②:同理可得:AE:BE=
.
综上可得:m=30°.
∠ABD=(180°-m)÷2=90°-
| 1 |
| 2 |
∠DBC=∠ABC-∠ABD=75°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |

(2)由分析图形可知m的取值为:
30°,120°,210°,300°,
故答案为:30°,120°,210°,300°;
(3)存在2个符合条件的m的值:m=30°或m=330°.
如图①:过E作EF⊥AB于F.
在Rt△BEF中,∵∠FBE=45°,
∴BE=
| 2 |

∵AE:BE=
| 2 |
∴AE=2EF;
又∵∠AFE=90°;
∴∠FAE=30°.即m=30°
在Rt△AEF中,∵∠FAE=30°,
∴AE=2EF,
∴AE:BE=
| 2 |
如图②:同理可得:AE:BE=
| 2 |
综上可得:m=30°.
点评:本题综合考查了等腰三角形的性质,等腰直角三角形的性质,旋转的性质,注意分类思想的运用,是考试压轴题,难度较大.

练习册系列答案
相关题目
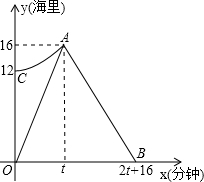 我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的
我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的 如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是
如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是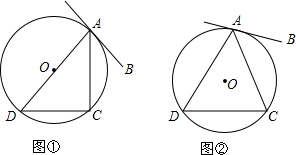 如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求:
如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求: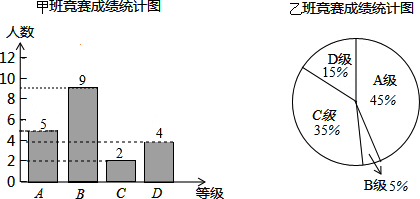
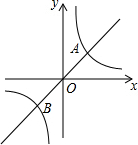 如图,定义:若双曲线y=
如图,定义:若双曲线y=