题目内容
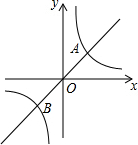 如图,定义:若双曲线y=
如图,定义:若双曲线y=| k |
| x |
| k |
| x |
| 1 |
| x |
(1)直接写出A、B两点的坐标;
(2)求双曲线y=
| 1 |
| x |
(3)若双曲线y=
| k |
| x |
| 2 |
考点:反比例函数与一次函数的交点问题
专题:新定义
分析:恩举反比例函数的他一一,可得答案.(1)根据解两函数解析式组成的方程组,可得答案;
(2)根据勾股定理,可得OA的长,根据A、B关于原点对称,可得答案;
(3)根据双曲线的对径,可得OA的长,根据解直角三角形,可得点A的坐标,
(2)根据勾股定理,可得OA的长,根据A、B关于原点对称,可得答案;
(3)根据双曲线的对径,可得OA的长,根据解直角三角形,可得点A的坐标,
解答:解:(1)A(1,1)B.(-1,-1)C
(2)直线y=x位置如图作AC⊥x轴
所以△OCA是等腰直角三角形,
即:OC=AC=1
OA=
=
AB=2OA=2
;
(3)∵双曲线的对径为10
,即AB=10
,OA=5
,
∴OA=
OC=
AC,
∴OC=AC=5,
∴点A坐标为(5,5),
把A(5,5)代入双曲线y=
(k>0),
得k=5×5=25,
即k的值为25;
(2)直线y=x位置如图作AC⊥x轴
所以△OCA是等腰直角三角形,
即:OC=AC=1
OA=
| OC2+AC2 |
| 2 |
AB=2OA=2
| 2 |
(3)∵双曲线的对径为10
| 2 |
| 2 |
| 2 |
∴OA=
| 2 |
| 2 |
∴OC=AC=5,
∴点A坐标为(5,5),
把A(5,5)代入双曲线y=
| k |
| x |
得k=5×5=25,
即k的值为25;
点评:本题考查了反比例函数与一次函数交点问题,解方程组得出交点的坐标,双曲线的对径关于原点对称.

练习册系列答案
相关题目
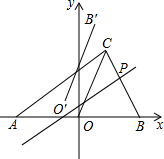 如图,Rt△ABC的斜边AB在x轴上,OA=OB=6,点C在第一象限,∠A=30°,P(m,n)是线段BC上的动点,过点P作BC的垂线a,以直线a为对称轴,将线段OB轴对称变换后得线段O′B′,
如图,Rt△ABC的斜边AB在x轴上,OA=OB=6,点C在第一象限,∠A=30°,P(m,n)是线段BC上的动点,过点P作BC的垂线a,以直线a为对称轴,将线段OB轴对称变换后得线段O′B′,
 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(d,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(d,2).