题目内容
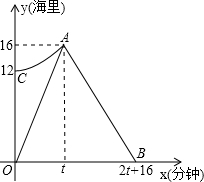 我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的
我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的| 2 |
| 3 |
(1)求救援船的前往速度;
(2)若该故障渔船在发出救援信号后40分钟内得不到营救就会有危险,请问救援船的前往速度每小时至少是多少海里,才能保证渔船的安全.
考点:二次函数的应用
专题:
分析:(1)根据图象可以看出轮船到出发点的距离是16海里,设救援船的前往速度为每分钟v海里,则返程速度为每分钟
v海里,由题意得出方程
=
-16,求出方程的解即可;
(2)求出抛物线的解析式,把x=40分钟代入求出即可.
| 2 |
| 3 |
| 16 |
| v |
| ||
|
(2)求出抛物线的解析式,把x=40分钟代入求出即可.
解答:解:(1)从图象可以看出轮船到出发点的距离是16海里,
即救援船行驶了16海里与故障船会合,
设救援船的前往速度为每分钟v海里,则返程速度为每分钟
v海里,
由题意得:
=
-16,
v=0.5,
经检验v=0.5是原方程的解,
答:该救援船的前往速度为每分钟0.5海里.
(2)由(1)知:t=16÷0.5=32,
则A(32,16),将A(32,16),C(0,12)代入y=ax2+k得:
,
解得
,
即y=
x2+12,
把x=40代入得:y=
×402+12=
,
÷
=
,
即救援船的前往速度为每小时至少是
海里.
即救援船行驶了16海里与故障船会合,
设救援船的前往速度为每分钟v海里,则返程速度为每分钟
| 2 |
| 3 |
由题意得:
| 16 |
| v |
| ||
|
v=0.5,
经检验v=0.5是原方程的解,
答:该救援船的前往速度为每分钟0.5海里.
(2)由(1)知:t=16÷0.5=32,
则A(32,16),将A(32,16),C(0,12)代入y=ax2+k得:
|
解得
|
即y=
| 1 |
| 256 |
把x=40代入得:y=
| 1 |
| 256 |
| 73 |
| 4 |
| 73 |
| 4 |
| 40 |
| 60 |
| 219 |
| 8 |
即救援船的前往速度为每小时至少是
| 219 |
| 8 |
点评:本题考查了二次函数的应用,关键是能根据题意列出算式或函数式,用了转化思想和数形结合思想.

练习册系列答案
相关题目
 如图,AB是圆O的直径,CD⊥AB于D点,AD=4cm,DB=9cm,求CB的长.
如图,AB是圆O的直径,CD⊥AB于D点,AD=4cm,DB=9cm,求CB的长. 如图,A是线段BF延长线上的点,矩形BCDF的外接圆O交AC的中点E.
如图,A是线段BF延长线上的点,矩形BCDF的外接圆O交AC的中点E. 已知抛物线 y=ax2+bx+c(a>0)的图象经过过点B(12,0)和C(0,6),对称轴方程为x=2.
已知抛物线 y=ax2+bx+c(a>0)的图象经过过点B(12,0)和C(0,6),对称轴方程为x=2. 如图,点O为∠APB角平分线上一点,半径为2的⊙O切PA于A点,AP=4.
如图,点O为∠APB角平分线上一点,半径为2的⊙O切PA于A点,AP=4. 如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是
如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 如图,Rt△ABC的斜边AB在x轴上,OA=OB=6,点C在第一象限,∠A=30°,P(m,n)是线段BC上的动点,过点P作BC的垂线a,以直线a为对称轴,将线段OB轴对称变换后得线段O′B′,
如图,Rt△ABC的斜边AB在x轴上,OA=OB=6,点C在第一象限,∠A=30°,P(m,n)是线段BC上的动点,过点P作BC的垂线a,以直线a为对称轴,将线段OB轴对称变换后得线段O′B′,