题目内容
已知关于x的一元二次方程:x2-(k+2)x+
k2+1=0.
(1)k取什么值时,原方程有两个不相等的实数根?
(2)如果方程的两个实数根x1、x2(x1<x2)满足x1+|x2|=4,求k的值和方程的两根.
| 1 |
| 4 |
(1)k取什么值时,原方程有两个不相等的实数根?
(2)如果方程的两个实数根x1、x2(x1<x2)满足x1+|x2|=4,求k的值和方程的两根.
考点:根的判别式,根与系数的关系
专题:计算题
分析:(1)根据判别式的意义得到△=(k+2)2-4(
k2+1)>0,然后解不等式得到k>0;
(2)根据根与系数的关系得x1+x2=k+2>0,x1•x2=
k2+1>0,则0<x1<x2,对x1+|x2|=4去绝对值得到x1+x2=4,所以k+2=4,解得k=2,当k=2时,原方程变形为x2-4x+2=0,然后利用配方法解方程.
| 1 |
| 4 |
(2)根据根与系数的关系得x1+x2=k+2>0,x1•x2=
| 1 |
| 4 |
解答:解:(1)根据题意得△=(k+2)2-4(
k2+1)>0,解得k>0,
即k>0时,原方程有两个不相等的实数根;
(2)根据题意得x1+x2=k+2>0,x1•x2=
k2+1>0,
∴0<x1<x2,
∴x1+x2=4,
∴k+2=4,解得k=2,
当k=2时,原方程变形为x2-4x+2=0,
x2-4x+4=2,
(x-2)2=2,
所以x1=2+
,x2=2-
.
| 1 |
| 4 |
即k>0时,原方程有两个不相等的实数根;
(2)根据题意得x1+x2=k+2>0,x1•x2=
| 1 |
| 4 |
∴0<x1<x2,
∴x1+x2=4,
∴k+2=4,解得k=2,
当k=2时,原方程变形为x2-4x+2=0,
x2-4x+4=2,
(x-2)2=2,
所以x1=2+
| 2 |
| 2 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了根与系数的关系.

练习册系列答案
相关题目
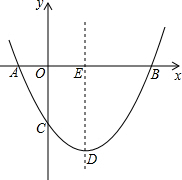 如图,抛物线y=
如图,抛物线y=| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是
如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是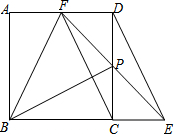 如图,在正方形ABCD中,点P是CD边上的点,连结BP,将△BCP绕点C按顺时针方向旋转90°,得到△DCE,连结EP并延长,交AD于点F,连结BF、FC.
如图,在正方形ABCD中,点P是CD边上的点,连结BP,将△BCP绕点C按顺时针方向旋转90°,得到△DCE,连结EP并延长,交AD于点F,连结BF、FC.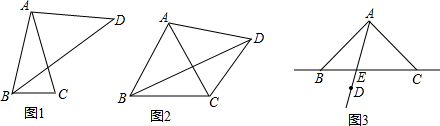
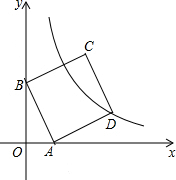 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=