题目内容
 如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD.
如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD.求证:AB=CD.
考点:全等三角形的判定与性质
专题:证明题
分析:由AB∥CD,得出∠BAD+∠D=∠B+∠BCD,再由∠B=∠D,得出∠BAD=∠BCD,进一步由∠1=∠2,∠3=∠4,推出∠1=∠4,利用AAS证得△ABF≌△CDE,结论成立.
解答:
证明:∵AB∥CD,
∴∠BAD+∠D=∠B+∠BCD,
∵∠B=∠D,
∴∠BAD=∠BCD,
∵∠1=∠2,∠3=∠4,
∴∠1=∠4,
在△ABF和△CDE中,
∴△ABF≌△CDE(AAS),
∴AB=CD.
∴∠BAD+∠D=∠B+∠BCD,
∵∠B=∠D,
∴∠BAD=∠BCD,
∵∠1=∠2,∠3=∠4,
∴∠1=∠4,
在△ABF和△CDE中,
|
∴△ABF≌△CDE(AAS),
∴AB=CD.
点评:此题考查三角形全等的判定与性质,平行线的性质,掌握基本的判定方法是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各式计算正确的是( )
| A、-(-42)=-16 | ||||||||
| B、-8-2×6=(-1+6)×(-2) | ||||||||
C、4÷
| ||||||||
| D、(-1)2013+(-1)2014=-1+1=0 |
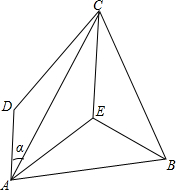 如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=120°.求∠DAC的度数α的值.
如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=120°.求∠DAC的度数α的值. 如图,过原点O任意引一直线交y=
如图,过原点O任意引一直线交y= 如图,在平面直角坐标系中,已知点A(0,4)、B(-4,0),BE⊥AC于E交y轴于点M(0,a),且∠BMA=105°.下列四个结论:①AE=
如图,在平面直角坐标系中,已知点A(0,4)、B(-4,0),BE⊥AC于E交y轴于点M(0,a),且∠BMA=105°.下列四个结论:①AE=