题目内容
在平行四边形ABCD中,AC的垂直平分线分别交CD、AB于点F、E,AB=4,BC=
,AC=3
,求EF.
| 3 |
| 3 |
考点:平行四边形的性质
专题:
分析:如图,过C作CG∥FE交AB的延长线于G、作CH⊥BG交BG于H.构建直角△AHC、直角△BCH,相似三角形△ACH∽△AGC,以及平行四边形EFCG.利用勾股定理和相似三角形的对应边成比例可以求得CG的长度,则平行四边形EFCG的对边相等:EF=CG.
解答:
解:如图,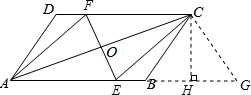 过C作CG∥FE交AB的延长线于G、作CH⊥BG交BG于H.
过C作CG∥FE交AB的延长线于G、作CH⊥BG交BG于H.
由勾股定理得到:CH2=AC2-(AB+BH)2=BC2-BH2,
∵AB=4,BC=
,AC=3
,
∴(3
)2-(4+BH)2=(
)2-BH2,
解得∴BH=1.
∴AH=AB+BH=4+1=5.
∴CH=
=
.
∵CG∥FE、AC⊥FE,
∴CG⊥AC.
∵∠CAH=∠GAC,∠AHC=∠ACG=90°,
∴△ACH∽△AGC,
∴CH:CG=AH:AC,
∴CG=
=
=
.
∵四边形ABCD平行四边形,
∴FC∥EG.
又CG∥FE,
∴四边形EFCG是平行四边形,
∴EF=CG=
.
 过C作CG∥FE交AB的延长线于G、作CH⊥BG交BG于H.
过C作CG∥FE交AB的延长线于G、作CH⊥BG交BG于H.由勾股定理得到:CH2=AC2-(AB+BH)2=BC2-BH2,
∵AB=4,BC=
| 3 |
| 3 |
∴(3
| 3 |
| 3 |
解得∴BH=1.
∴AH=AB+BH=4+1=5.
∴CH=
| AC2-AH2 |
| 2 |
∵CG∥FE、AC⊥FE,
∴CG⊥AC.
∵∠CAH=∠GAC,∠AHC=∠ACG=90°,
∴△ACH∽△AGC,
∴CH:CG=AH:AC,
∴CG=
| CH•AC |
| AH |
| ||||
| 5 |
3
| ||
| 5 |
∵四边形ABCD平行四边形,
∴FC∥EG.
又CG∥FE,
∴四边形EFCG是平行四边形,
∴EF=CG=
3
| ||
| 5 |
点评:本题考查了平行四边形的性质.解题时利用了勾股定理、相似三角形的判定与性质以及平行四边形的判定与性质,综合性比较强,难度较大.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
下列各数中,是无理数的为( )
A、
| |||
| B、3.14 | |||
C、
| |||
D、-
|
如图所示,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②∠A=∠D;∠B=∠E,∠C=∠F;③AB=DE,BC=EF,∠B=∠E;④AB=DE,∠C=∠F,AC=DF.其中能使△ABC≌△DEF的条件的组数共有( )
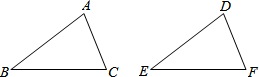

| A、1组 | B、2组 | C、3组 | D、4组 |
 如图,在平面直角坐标系中,已知点A(0,4)、B(-4,0),BE⊥AC于E交y轴于点M(0,a),且∠BMA=105°.下列四个结论:①AE=
如图,在平面直角坐标系中,已知点A(0,4)、B(-4,0),BE⊥AC于E交y轴于点M(0,a),且∠BMA=105°.下列四个结论:①AE=| 1 |
| 2 |
| A、只有①④ | B、只有①③④ |
| C、只有②③ | D、①②③④ |
已知二次函数y=kx2-2x-1(k≠0)的图象与x轴有两个交点,则k的取值范围是( )
| A、k>-1且k≠0 |
| B、k>-1 |
| C、k<1且k≠0 |
| D、k<1 |
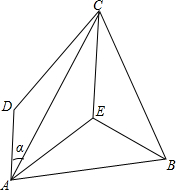 如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=120°.求∠DAC的度数α的值.
如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=120°.求∠DAC的度数α的值. 如图,过原点O任意引一直线交y=
如图,过原点O任意引一直线交y=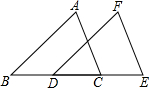 如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.