题目内容
15. 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )| A. | 12cm | B. | 6cm | C. | 3$\sqrt{2}$cm | D. | 2$\sqrt{3}$cm |
分析 圆的半径为12,求出AB的长度,用弧长公式可求得弧BC的长度,圆锥的底面圆的半径=圆锥的弧长÷2π.
解答 解:AB=$\frac{BC}{\sqrt{2}}$=$\frac{24}{\sqrt{2}}$=12$\sqrt{2}$cm,
∴$\widehat{BC}$=$\frac{90π×12\sqrt{2}}{180}$=6$\sqrt{2}$π
∴圆锥的底面圆的半径=6$\sqrt{2}$π÷(2π)=3$\sqrt{2}$cm.
故选C.
点评 本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
5.计算|-2|的结果是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
4.计算:(-2x)3=( )
| A. | 6x3 | B. | -6x3 | C. | -8x3 | D. | 8x3 |
 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )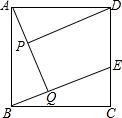 已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.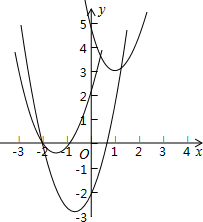 在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+5经过点M(1,3)和N(3,5)
在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+5经过点M(1,3)和N(3,5) 如图,平行四边形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件AC⊥BD或∠AOB=90°或AB=BC使其成为菱形(只填一个即可).
如图,平行四边形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件AC⊥BD或∠AOB=90°或AB=BC使其成为菱形(只填一个即可).