��Ŀ����
��ͼ��ʾ���ڡ�ABC�У�AB��AC����D��AC�ϣ���BD��BC��AD�����A����( )
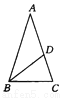
A. 30�� B. 40�� C. 45�� D. 36��
 D
����������AD��BD��
���A����ABD��
���BDC��2��A.
��BD��BC��
���C����BDC��2��A��
��AB��AC��
���ABC����C��2��A��
���������ڽǺͶ������á�A+2��A+2��A��180�㣬
����A��36�㣮
��ѡD.
D
����������AD��BD��
���A����ABD��
���BDC��2��A.
��BD��BC��
���C����BDC��2��A��
��AB��AC��
���ABC����C��2��A��
���������ڽǺͶ������á�A+2��A+2��A��180�㣬
����A��36�㣮
��ѡD.
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
��ͼ����AE�۵�����ֽƬABCD��ʹ��D����BC�ߵĵ�F����֪AB=8��BC=10����tan��EFC��ֵΪ��������
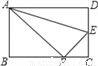
A. 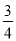 B.
B. 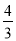 C.
C. 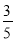 D.
D. 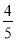
 A
�������������������������ɵã���Rt��ABF�У���AB=8��AF=AD=10��BF=6��
��Rt��ABF��Rt��EFC������EFC=��BAF����tan��EFC=tan��BAF=��
��ѡA��
A
�������������������������ɵã���Rt��ABF�У���AB=8��AF=AD=10��BF=6��
��Rt��ABF��Rt��EFC������EFC=��BAF����tan��EFC=tan��BAF=��
��ѡA�� ��һ��ֱ���������У���һ����ǵ���30�㣬����һ����ǵĴ�СΪ______�ȣ�
 60
����������������
����������ֱ�������Σ�һ����ǵ���30�㣬����һ�����Ϊ90�㩁30��=60�㣮
�ʴ�Ϊ��60��
60
����������������
����������ֱ�������Σ�һ����ǵ���30�㣬����һ�����Ϊ90�㩁30��=60�㣮
�ʴ�Ϊ��60�� ��һ��ֱ�����dz���ͼ���ã�����AOD=20�㣬 ���BOC�Ĵ�СΪ�� ��
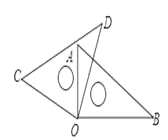
A. 140�� B. 160�� C. 170�� D. 150��
 B
��������������������ݡ�AOD=20��ɵã���AOC=70�㣬��������ɵã���BOC=��AOB+��AOC=90��+70��=160��.
B
��������������������ݡ�AOD=20��ɵã���AOC=70�㣬��������ɵã���BOC=��AOB+��AOC=90��+70��=160��. ���������εĶ��Ǧ���90�㣬������䶥�ǵĶ�����һ��ֱ�߽�������������η� �����������������Σ���ô���Ķ���Ϊ________��
 108��
����������ͼ��
��AB=AC��BD=AD��AC=CD��
���1=��B����2=��4����B=��C��
�ߡ�4=��1+��B=2��B=2��C��
���2=��4=2��C��
�ߡ�2+��4+��C=180�㣬
��5��C=180�㣬
���C=36�㣬
���=��BAC=180��-2��C=108�㣮
108��
����������ͼ��
��AB=AC��BD=AD��AC=CD��
���1=��B����2=��4����B=��C��
�ߡ�4=��1+��B=2��B=2��C��
���2=��4=2��C��
�ߡ�2+��4+��C=180�㣬
��5��C=180�㣬
���C=36�㣬
���=��BAC=180��-2��C=108�㣮 ��ͼ����ABC��MN����ƽ��3cm��Ϊ��DEF��ô��A�Ķ�Ӧ�����ĸ��㣿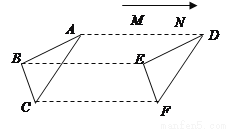
 D��.
�������������������ABC��MN����ƽ��3cm��Ϊ��DEF�����ɵõ���Ӧ��Ĺ�ϵ.���������A����MN�ķ���ƽ��3cm���Ӧ����D��.
D��.
�������������������ABC��MN����ƽ��3cm��Ϊ��DEF�����ɵõ���Ӧ��Ĺ�ϵ.���������A����MN�ķ���ƽ��3cm���Ӧ����D��. ƽ�Ʋ��ı�ͼ�ε� ___________�� ___________
 ��״ ��С
�����������������ƽ�Ʋ��ı�ͼ�ε���״�ʹ�С.
�ʴ�Ϊ��(1). ��״ (2). ��С.
��״ ��С
�����������������ƽ�Ʋ��ı�ͼ�ε���״�ʹ�С.
�ʴ�Ϊ��(1). ��״ (2). ��С. ������ʽax-2��0�Ľ⼯Ϊx��-2�������y�ķ���ay+2=0�Ľ�
 2
��������������������ݲ���ʽax-2��0�Ľ⼯Ϊx��-2����ȷ��a��ֵ��Ȼ����뷽�̣��ⷽ����ã�
����������߲���ʽax-2��0����ax��2�Ľ⼯Ϊx��-2��
��a=-1��
���뷽�̵ã�-y+2=0��
��ã�y=2��
2
��������������������ݲ���ʽax-2��0�Ľ⼯Ϊx��-2����ȷ��a��ֵ��Ȼ����뷽�̣��ⷽ����ã�
����������߲���ʽax-2��0����ax��2�Ľ⼯Ϊx��-2��
��a=-1��
���뷽�̵ã�-y+2=0��
��ã�y=2�� �ֽ���ʽ�� 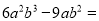 _______
_______
 �������������ṫ��ʽ���ֽ���ʽ���ɵ�=.
�ʴ�Ϊ�� .
�������������ṫ��ʽ���ֽ���ʽ���ɵ�=.
�ʴ�Ϊ�� . 
