题目内容
16.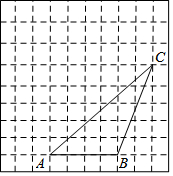 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.(1)在图中画出平移后△A'B'C';
(2)连接AA',CC',则这两条线段的关系是相等且平行;
(3)画出△ABC的AB边上的高CD和AC边上的中线BE.
分析 (1)根据平移画图;
(2)由平移的性质得:?AA′C′C,可得结论;
(3)如图3,画出高线CD和中线BE.
解答  解:(1)如图1,
解:(1)如图1,
(2)AA',CC'的关系是相等且平行,
理由是:如图2,由平移得:AC=A′C′,AC∥A′C′,
∴四边形AA′C′C是平行四边形,
∴AA′=CC′,AA′∥CC′,
故答案为:相等且平行;
(3)如图3所示,
点评 本题考查了作图-平移变换、平行四边形的性质和判定、三角形的高线和中线的定义,熟练掌握平移的定义及性质,明确三角形高线和中线的定义,属于基础题.

练习册系列答案
相关题目
16.一个两位数,十位上的数字是x,个位上的数字是y,把这个两位数十位上数字与个位上数字调换位置后的两位数用代数式表示为( )
| A. | yx | B. | xy | C. | 10y+x | D. | 10x+y |
1.已知a2+b2=$\frac{2}{3}a-6b-\frac{82}{9}$,则ab=( )
| A. | -1 | B. | 27 | C. | 9 | D. | 3 |
 小明在荡秋千时,发观秋千在静止时,秋千离地面3dm(EF=3dm),荡起的水平距离为13dm(BC=13dm)时,离地面8dm(BD=8dm),求秋千的绳索AF的长.
小明在荡秋千时,发观秋千在静止时,秋千离地面3dm(EF=3dm),荡起的水平距离为13dm(BC=13dm)时,离地面8dm(BD=8dm),求秋千的绳索AF的长.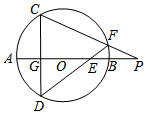 (如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2.
(如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2.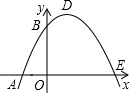 如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)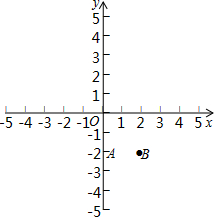 在如图的平面直角坐标系xOy中,抛物线y=2x2+bx+c经过点A(0,-2),B(2,-2).
在如图的平面直角坐标系xOy中,抛物线y=2x2+bx+c经过点A(0,-2),B(2,-2).