题目内容
15.如图1,在边长为2的正方形ABCD中,P是对角线BD上的动点,点E在射线AD上,且PA=PE.(1)求证:PC=PE;
(2)求∠EPC的度数;
(3)如图2,把正方形ABCD改为边长为2的菱形ABCD,且∠ABC=120°,其他条件不变,连接CE,求AP•CE的最小值.
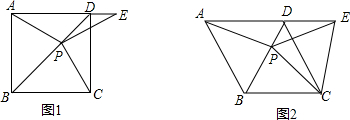
分析 (1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法易证△EPC是等边三角形,由等边三角形的性质可得AP=CE,当AP•CE的值最小时,则AP最小,由垂线段最短可知当AP⊥BD时,AP最小,利用勾股定理求出AP的值即可得到两条线段乘积的最小值.
解答 (1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABP=∠CBP}\\{PB=PB}\end{array}\right.$,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABP=∠CBP}\\{PB=PB}\end{array}\right.$,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE,
当AP•CE的值最小时,则AP最小,由垂线段最短可知当AP⊥BD时,AP最小,此时AP=$\sqrt{A{B}^{2}-B{P}^{2}}$=$\sqrt{3}$,
∴AP•CE的最小值=$\sqrt{3}$×$\sqrt{3}$=3.
点评 本题考查了正方形的性质,全等三角形的判定与性质,菱形的性质,等边三角形的判定和性质,熟记正方形的性质确定出∠ABP=∠CBP是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 3.77×103 | B. | 3.77×1010 | C. | 3.77×1011 | D. | 3.77×1012 |
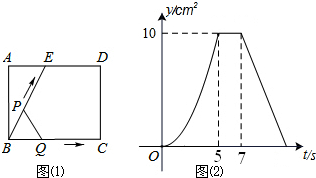 如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图(2),当t=$\frac{29}{4}$秒时,△ABE与△BQP相似.
如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图(2),当t=$\frac{29}{4}$秒时,△ABE与△BQP相似.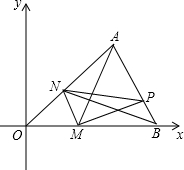 如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.
如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.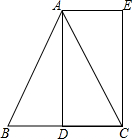 已知,如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.
已知,如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.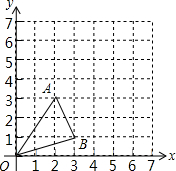 如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大到原来的2倍后得到△OA′B′,其中A、B在图中格点上,点A、B的对应点分别为A′、B′.
如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大到原来的2倍后得到△OA′B′,其中A、B在图中格点上,点A、B的对应点分别为A′、B′.