题目内容
2.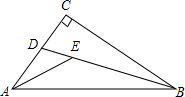 直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.
直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.
分析 根据三角形的内角和等于180°求出∠BAC+∠ABC,再根据角平分线的定义求出∠EAB+∠EBA,然后根据三角形的一个外角等于与它不相邻的两个内角的和可得∠DEA=∠EAB+∠EBA,从而得解.
解答 解:∵∠C=90°,
∴∠BAC+∠ABC=180°-90°=90°,
∵AE、BD分别是∠CAB、∠CBA的角平分线,
∴∠EAB=$\frac{1}{2}$∠BAC,∠EBA=$\frac{1}{2}$∠ABC,
∴∠EAB+∠EBA=$\frac{1}{2}$(∠BAC+∠ABC)=$\frac{1}{2}$×90°=45°,
由三角形的外角性质得,∠DEA=∠EAB+∠EBA=45°.
故答案为:45.
点评 本题考查了三角形的内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12. 如图,?ABCD中,E为AB中点,CE交BD于F,若△CBE的面积为S,则△DCF的面积为( )
如图,?ABCD中,E为AB中点,CE交BD于F,若△CBE的面积为S,则△DCF的面积为( )
 如图,?ABCD中,E为AB中点,CE交BD于F,若△CBE的面积为S,则△DCF的面积为( )
如图,?ABCD中,E为AB中点,CE交BD于F,若△CBE的面积为S,则△DCF的面积为( )| A. | $\frac{2}{3}S$ | B. | S | C. | $\frac{4}{3}S$ | D. | 2S |
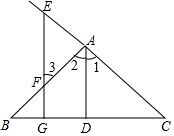 如图,已知AD⊥BC,EG⊥BC,若∠E=∠3.则AD平分∠BAC.(填空)
如图,已知AD⊥BC,EG⊥BC,若∠E=∠3.则AD平分∠BAC.(填空)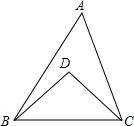 如图所示,在△ABC中,∠A=60°,点D在△ABC的内部,并且∠DBA=$\frac{1}{4}$∠ABC,∠DCA=$\frac{1}{4}$∠ACB,则∠D的度数是90°.
如图所示,在△ABC中,∠A=60°,点D在△ABC的内部,并且∠DBA=$\frac{1}{4}$∠ABC,∠DCA=$\frac{1}{4}$∠ACB,则∠D的度数是90°. 如图,折叠宽度相等的长方形纸条,若∠1=60°,则∠2=60度.
如图,折叠宽度相等的长方形纸条,若∠1=60°,则∠2=60度.