题目内容
10.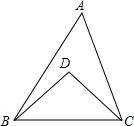 如图所示,在△ABC中,∠A=60°,点D在△ABC的内部,并且∠DBA=$\frac{1}{4}$∠ABC,∠DCA=$\frac{1}{4}$∠ACB,则∠D的度数是90°.
如图所示,在△ABC中,∠A=60°,点D在△ABC的内部,并且∠DBA=$\frac{1}{4}$∠ABC,∠DCA=$\frac{1}{4}$∠ACB,则∠D的度数是90°.
分析 首先根据∠A的度数求得另外两个角的和,然后根据角之间的数量关系求解.
解答 解:∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵∠DBA=$\frac{1}{4}$∠ABC,∠DCA=$\frac{1}{4}$∠ACB,
∴∠DBC+∠DCB=$\frac{3}{4}$(∠ABC+∠ACB)=$\frac{3}{4}$×120°=90°,
∴∠D=90°.
故答案为:90°.
点评 本题考查了三角形的内角和定理,解题的关键是能够确定△BDC是直角三角形,难度不大.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
5.1-4个月的婴儿生长发育非常快,他们的体重y(g)与月龄x(月)间的关系如表所示.
请写出y与x之间的关系式y=700x+3500.
请写出y与x之间的关系式y=700x+3500.
| 月龄/月 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 体重/g | 3500 | 4200 | 4900 | 5600 | 6300 | 7000 | 7700 |
15.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如表所示的优惠.例如:购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数多于60次时,则最省钱的方式为( )
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
19.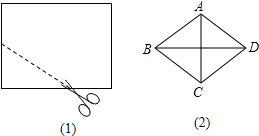 如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
 如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )| A. | 10cm2 | B. | 20cm2 | C. | 40cm2 | D. | 80cm2 |
20.下列各对数中,互为相反数的是( )
| A. | +(-2)和-(+2) | B. | -|-3|和+(-3) | C. | (-1)2和-12 | D. | (-1)3和-13 |

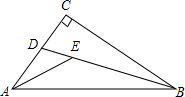 直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.
直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.