题目内容
7.$\sqrt{2}$+$\sqrt{3}$的有理化因式是$\sqrt{2}$-$\sqrt{3}$.分析 根据平方差公式即可得出($\sqrt{2}$+$\sqrt{3}$)×($\sqrt{2}$-$\sqrt{3}$)=-1,再结合有理化因式的定义即可得出结论.
解答 解:∵($\sqrt{2}$+$\sqrt{3}$)×($\sqrt{2}$-$\sqrt{3}$)=$(\sqrt{2})^{2}$-$(\sqrt{3})^{2}$=2-3=-1,
∴$\sqrt{2}$-$\sqrt{3}$是$\sqrt{2}$+$\sqrt{3}$的一个有理化因式.
故答案为:$\sqrt{2}$-$\sqrt{3}$.
点评 本题考查了平方差公式以及有理化因式的定义,根据平方差公式找出($\sqrt{2}$+$\sqrt{3}$)×($\sqrt{2}$-$\sqrt{3}$)=-1是解题的关键.

练习册系列答案
相关题目
15.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如表所示的优惠.例如:购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数多于60次时,则最省钱的方式为( )
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
12.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
则当y>2时,x的取值范围是x<1或x>3.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
19.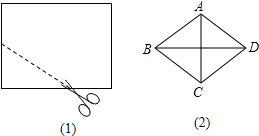 如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
 如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )| A. | 10cm2 | B. | 20cm2 | C. | 40cm2 | D. | 80cm2 |

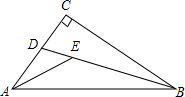 直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.
直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.