题目内容
12. 如图,?ABCD中,E为AB中点,CE交BD于F,若△CBE的面积为S,则△DCF的面积为( )
如图,?ABCD中,E为AB中点,CE交BD于F,若△CBE的面积为S,则△DCF的面积为( )| A. | $\frac{2}{3}S$ | B. | S | C. | $\frac{4}{3}S$ | D. | 2S |
分析 先得到CD=2BE,从而得出S△CDE=2S,再求出$\frac{EF}{CF}=\frac{BE}{CD}=\frac{1}{2}$,得出$\frac{{S}_{△DEF}}{{S}_{△CDF}}=\frac{EF}{CF}$=$\frac{1}{2}$,即:$\frac{{S}_{△CDE}}{{S}_{△CDF}}=\frac{3}{2}$,即可得出结论.
解答 解:如图,过点A作AG⊥CD,
∵E为AB中点,
∴BE=$\frac{1}{2}$AB,
在?ABCD中,AB=CD,
∴CD=2BE,
∵S△BCE=$\frac{1}{2}$BE×AG=S,S△CDE=$\frac{1}{2}$CD×AG=$\frac{1}{2}$×2BE×AG,
∴S△CDE=2S,
∵BE∥CD,
∴$\frac{EF}{CF}=\frac{BE}{CD}=\frac{1}{2}$,
∴$\frac{{S}_{△DEF}}{{S}_{△CDF}}=\frac{EF}{CF}$=$\frac{1}{2}$,
∴$\frac{{S}_{△CDE}}{{S}_{△CDF}}=\frac{3}{2}$,
∴S△CDF=$\frac{2}{3}$×S△CDE=$\frac{4}{3}$S,
故选:C.
点评 此题是平行四边形的性质,主要考查了平行四边形的性质,同高的两三角形面积比是底的比,解本题的关键是得出$\frac{{S}_{△CDE}}{{S}_{△CDF}}=\frac{3}{2}$,.

练习册系列答案
相关题目
20.下列各对数中,互为相反数的是( )
| A. | +(-2)和-(+2) | B. | -|-3|和+(-3) | C. | (-1)2和-12 | D. | (-1)3和-13 |
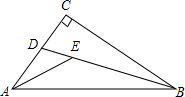 直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.
直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.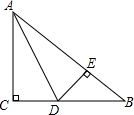 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且△ACD的周长为30,AD=13cm,则斜边AB长为17cm.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且△ACD的周长为30,AD=13cm,则斜边AB长为17cm.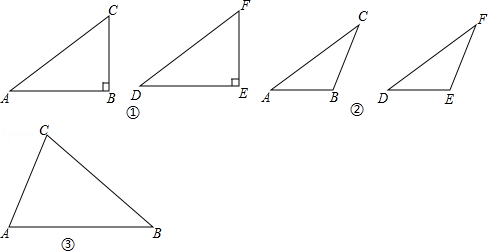
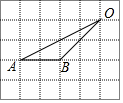 如图,正方形网格中每个小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的余弦值是$\frac{2\sqrt{5}}{5}$.
如图,正方形网格中每个小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的余弦值是$\frac{2\sqrt{5}}{5}$.