题目内容
5.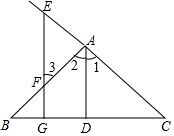 如图,已知AD⊥BC,EG⊥BC,若∠E=∠3.则AD平分∠BAC.(填空)
如图,已知AD⊥BC,EG⊥BC,若∠E=∠3.则AD平分∠BAC.(填空)证明:∵AD⊥BC,EG⊥BC(已知)
∴AD∥EG(在同一平面内,垂直于同一直线的两直线平行)
∴∠1=∠E(两直线平行,同位角相等)
∠2=∠3(两直线平行,内错角相等)
∵∠E=∠3(已知)
∴∠1=,2(等量代换)
即AD平分∠BAC.
分析 先根据已知条件推出AD∥EF,再由平行线的性质得出∠1=∠2,∠3=∠E,结合已知通过等量代换即可得到∠1=∠2,根据角平分线的定义可知AD是∠BAC的平分线.
解答  证明:∵AD⊥BC,EG⊥BC(已知)
证明:∵AD⊥BC,EG⊥BC(已知)
∴AD∥EG(在同一平面内,垂直于同一直线的两直线平行)
∴∠1=∠E(两直线平行,同位角相等)
∠2=_∠3_(两直线平行,内错角相等)
∵∠E=∠3(已知)
∴∠1=∠2(等量代换)
即AD平分∠BAC.
故答案为:在同一平面内,垂直于同一直线的两直线平行,两直线平行,同位角相等,两直线平行,内错角相等,∠2.
点评 本题考查的是平行线的判定及性质,属较简单题目.

练习册系列答案
相关题目
15.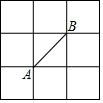 如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
 如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )| A. | 6 个 | B. | 7 个 | C. | 8 个 | D. | 9个 |
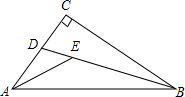 直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.
直角△ABC中,∠C=90°,AE、BD分别是∠CAB、∠CBA的角平分线,则∠DEA=45°.