题目内容
19.某商场以每个80元的价格进了一批玩具,当售价为120元时,商场平均每天可售出20个.为了扩大销售,增加盈利,商场决定采取降价措施,经调查发现:在一定范围内,玩具的单价每降低1元,商场每天可多售出2个.设每个玩具售价下降了x元,但售价不得低于玩具的进价,商场每天的销售利润为y元.(1)降价后商场平均每天可售出20+2x个玩具;
(2)求y与x的函数表达式,并直接写出自变量x的取值范围;
(3)商场将每个玩具的售价定为多少元时,可使每天获得的利润最大?最大利润是多少元?
分析 (1)根据:降价后销量=降价前销量+增加的销量,列出代数式;
(2)根据:每天的总利润=每个玩具利润×降价后每天的销售数量,可列出y关于x的函数关系式;根据降价后价格不小于进价,确定x的范围;
(3)将(2)中函数表达式配方成顶点式,结合x的范围可求出最大利润.
解答 解:(1)降价后商场平均每天可售出玩具数量为:20+2x;
(2)由题意得y=(120-x-80)(20+2x)=-2x2+60x+800,其中,x的取值范围是0<x≤40;
(3)y=-2x2+60x+800=-2(x-15)2+1250(0<x≤40),
∴当x=15时,y有最大值1250.
此时玩具的售价为120-15=105(元).
∴该商场将每个玩具的售价定为105元时,可使每天获得的利润最大,最大利润是1250元.
故答案为:(1)20+2x.
点评 本题考查了利用二次函数解决实际问题能力,主要利用了利润=每个玩具的利润×销售量,求函数的最值时,应注意自变量的取值范围.

练习册系列答案
相关题目
 如图,l1∥l2,AB∥CD,BC=2CF.若△CEF的面积是5,求四边形ABCD的面积.
如图,l1∥l2,AB∥CD,BC=2CF.若△CEF的面积是5,求四边形ABCD的面积.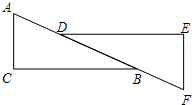 如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE.
如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE. 如图,△ABC中,BD⊥AC于D,CE⊥AB于E,BD=CE.求证:△ABC是等腰三角形.
如图,△ABC中,BD⊥AC于D,CE⊥AB于E,BD=CE.求证:△ABC是等腰三角形. 已知正六边形的边长为4cm,分别以它的三个不相邻的顶点为圆心,边长为半径画弧(如图),则所得到的三条弧的长度之和为8πcm.(结果保留π)
已知正六边形的边长为4cm,分别以它的三个不相邻的顶点为圆心,边长为半径画弧(如图),则所得到的三条弧的长度之和为8πcm.(结果保留π) 如图,在△ABC中,BD是∠ABC的平分线,CD是∠ACE的平分线,试探索∠D与∠A的数量关系,并说明理由.
如图,在△ABC中,BD是∠ABC的平分线,CD是∠ACE的平分线,试探索∠D与∠A的数量关系,并说明理由.