题目内容
3.我国第一艘航空母舰“辽宁号“在海上服役,舰载机在空中飞行执行任务,需要舰上的空中加油机给补充油,如图甲所示,在空中加油过程中,设舰载机的油箱中的余油量Q1吨,加油飞机的加油油箱中的余油量为Q2吨,加油时间为t分钟Q1、Q2与t之间的函数图象如图甲所示.请回答下列问题:(1)加油飞机的加油箱中装载了5.2吨油,将这些油全部加给舰载机需要5分钟;
(2)求加油过程中,舰载机的油箱中的余油量Q1(吨)与时间t(分钟)的函数关系式(并直接写出自变量的取值范围);
(3)求从加油开始经过几分钟加油机的油箱中的余油量与舰载机中的余油量相同;
(4)从加完油开始(此时舰载机在空中距航空母舰700千米),航空母舰以200千米/小时向东航行,而舰载机则以800千米/小时向西飞行执行任务,舰载机距航空母舰的距离为y,飞行时间为x,则y与x之间的函数图象如图乙所示.在不能再次空中加油的情况下,为了保证舰载机安全的降落航空母舰上,一定时间必须返回.求a的最大值.

分析 (1)观察图甲,寻找t=0时,Q2的值;寻找Q2=0时,t的值,由此得出结论;
(2)设舰载机的油箱中的余油量Q1(吨)与时间t(分钟)的函数关系式为Q1=kt+b,结合点的坐标利用待定系数法求出函数解析式;
(3)同(2)先求出加油飞机的油箱中的余油量Q2(吨)与时间t(分钟)的函数关系式,再令Q1=Q2,求出时间t即可;
(4)结合图甲找出舰载机的油耗,根据此油耗得出其续航时间,再根据“时间=路程÷速度”列出关于a的一元一次方程,解方程即可得出结论.
解答 解:(1)结合图甲可知:当t=0时,Q2的值为5.2;
当Q2的值为0时,t=5.
故答案为:5.2;5.
(2)设舰载机的油箱中的余油量Q1(吨)与时间t(分钟)的函数关系式为Q1=kt+b,
将点(0,1),(5,6)代入Q1=kt+b得,
$\left\{\begin{array}{l}{1=b}\\{6=5k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$.
故加油过程中,舰载机的油箱中的余油量Q1(吨)与时间t(分钟)的函数关系式为Q1=t+1(0≤t≤5).
(3)设加油飞机的油箱中的余油量Q2(吨)与时间t(分钟)的函数关系式为Q2=mt+n,
将点(0,5.2),(5,0)代入到Q2=mt+n得,
$\left\{\begin{array}{l}{5.2=n}\\{0=5m+n}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-1.04}\\{n=5.2}\end{array}\right.$,
故加油过程中,加油飞机的油箱中的余油量Q2(吨)与时间t(分钟)的函数关系式为Q2=-1.04t+5.2.
令Q1=Q2,即t+1=-1.04t+5.2,
解得:t=$\frac{105}{51}$.
故从加油开始经过$\frac{105}{51}$分钟加油机的油箱中的余油量与舰载机中的余油量相同.
(4)结合图甲可知:舰载机5分钟的耗油量为5.2-(6-1)=0.2(吨),
舰载机能够续航时间为6÷0.2×5=150(分).
结合题意可知:a+$\frac{700+(800+200)×\frac{a}{60}}{800-200}$×60=150,
解得:a=30.
故a的最大值为30分钟.
点评 本题考查了一次函数的应用、待定系数法求函数解析式以及解一元一次方程,解题的关键是:(1)观察图甲找出结论;(2)利用待定系数法求函数解析式;(3)解关于t的一元一次方程;(4)解关于a的一元一次方程.本题属于中档题,(1)(2)(3)难度不大,(4)稍微有点难度,在图甲中含有隐含条件“舰载机5分钟的耗油量为0.2吨”,再根据此条件求出舰载机的续航时间,结合数量关系即可列出关于a的一元一次方程.

| A. | x>2 | B. | x<1 | C. | 1<x≤2 | D. | 无解 |
 如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
 如图,在矩形纸片ABCD中,BC=40cm,AB=16cm,M点为BC边上的中点,点G沿B→A→D运动(不含端点),将矩形纸片沿直线MG翻折,使得点B落在AD边上,则折痕长度为10$\sqrt{5}$cm或8$\sqrt{5}$cm.
如图,在矩形纸片ABCD中,BC=40cm,AB=16cm,M点为BC边上的中点,点G沿B→A→D运动(不含端点),将矩形纸片沿直线MG翻折,使得点B落在AD边上,则折痕长度为10$\sqrt{5}$cm或8$\sqrt{5}$cm.
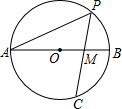 如图,在⊙O中,AB为直径,PC为弦,且PA=PC,PC交AB于M,若∠APC=45°,求$\frac{AM}{BM}$的值.
如图,在⊙O中,AB为直径,PC为弦,且PA=PC,PC交AB于M,若∠APC=45°,求$\frac{AM}{BM}$的值.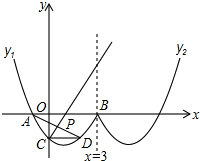 如图形似“w”的函数是由抛物线y1的一部分,其表达式为:y1=$\frac{\sqrt{3}}{3}$(x2-2x-3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
如图形似“w”的函数是由抛物线y1的一部分,其表达式为:y1=$\frac{\sqrt{3}}{3}$(x2-2x-3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.