题目内容
5.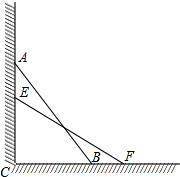 如图,一个长为5m的梯子斜靠在墙上,梯子的底端距墙4m.
如图,一个长为5m的梯子斜靠在墙上,梯子的底端距墙4m.(1)求梯子的顶端距地面的垂直距离;
(2)若将梯子的底端向墙推进1m,求梯子的顶端升高了多少米;
(3)若使梯子的顶端距地面4.8m,此时应将梯子再向墙推进多少米?
分析 (1)在直角三角形ECF中,利用勾股定理AC即可;
(2)在直角三角形BC中,利用勾股定理计算出AC长即可;
(3)首先计算出AC=4.8m时BC的长度,然后再根据题意得到应将梯子再向墙推进的距离.
解答 解:(1)由题意得:EF=5m,CF=4m,
则EC=$\sqrt{E{F}^{2}-C{F}^{2}}$=$\sqrt{25-16}$=3(m).
答:梯子的顶端距地面的垂直距离是3m;
(2)由题意得:BF=1m,则CB=4-1=3(m),
AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{25-9}$=4(m),
则AE=AC-EC=1m.
答:梯子的顶端升高了1m;
(3)若AC=4.8m,则BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-4.{8}^{2}}$=1.4(m),
应将梯子再向墙推进3-1.4=1.6(m).
答:应将梯子再向墙推进1.6m.
点评 此题主要考查了勾股定理的应用,关键是掌握从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
17.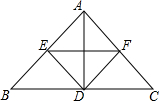 如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
 如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )| A. | 8个 | B. | 10个 | C. | 12个 | D. | 13个 |
 设有理数a,b,c在数轴上的对应点如图所示,|a|<|c|,化简|b-a|+|a+c|+|c-b|.
设有理数a,b,c在数轴上的对应点如图所示,|a|<|c|,化简|b-a|+|a+c|+|c-b|. 已知如图,△ABC是等边三角形,DE∥BC,交AB、AC于D、E,试说明△ADE是等边三角形.
已知如图,△ABC是等边三角形,DE∥BC,交AB、AC于D、E,试说明△ADE是等边三角形. 如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想:
如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想: