题目内容
17.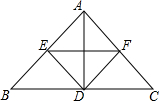 如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )| A. | 8个 | B. | 10个 | C. | 12个 | D. | 13个 |
分析 根据等腰直角三角形的判定定理即可得到结论.
解答  解:∵AB⊥AC,点D是BC的中点,AD⊥BC,
解:∵AB⊥AC,点D是BC的中点,AD⊥BC,
∴AB=AC,AD=BD,AD=CD,
∴△ABC,△ADB,△ADC是等腰直角三角形,
同理△BDE,△ADE,△ADF,△CDF是等腰直角三角形,
∵DE=AE,DF=AF,AE=AF,∠EAF=90°,
∴四边形AEDF是正方形,
∴△AOE,△AOF,△DOE,△DOF,△AEF,△EFD是等腰直角三角形,
∴图中等腰直角三角形的个数是13个.
故选D.
点评 本题考查了等腰直角三角形的判定,熟练掌握等腰直角三角形的判定定理是解题的关键.

练习册系列答案
相关题目
8.某旅行社要接团去外地旅游,经计算所获营业额y(元)与旅行团人数x(人)满足关系式y=-2x2+200x+2500,要使所获营业额最大,则此旅行团应有( )
| A. | 30人 | B. | 40人 | C. | 50人 | D. | 55人 |
2.作函数y=-x2的图象,并根据图象回答问题.
(1)列表:
(2)描点作图:
(3)函数y=-x2的图象是一条抛物线,开口向下,对称轴为y(x或y)轴,顶点坐标是(0,0),函数有最大(大或小)值0.
(4)在函数y=-x2中,当x>0时,若x1>x2,函数值y1<y2;当x<0时,若x1>x2,函数值y1>y2.
(1)列表:
| x | … | -3 | 0 | 1 | 2 | … | |||
| y=-x2 | … | -4 | -1 | -9 | … |

(3)函数y=-x2的图象是一条抛物线,开口向下,对称轴为y(x或y)轴,顶点坐标是(0,0),函数有最大(大或小)值0.
(4)在函数y=-x2中,当x>0时,若x1>x2,函数值y1<y2;当x<0时,若x1>x2,函数值y1>y2.
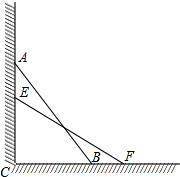 如图,一个长为5m的梯子斜靠在墙上,梯子的底端距墙4m.
如图,一个长为5m的梯子斜靠在墙上,梯子的底端距墙4m.
 如图,某居民小区要在一块一边靠墙(墙长20m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为50m的栅栏围成,设花园的BC边长为x(m),花园的面积为S(m2).
如图,某居民小区要在一块一边靠墙(墙长20m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为50m的栅栏围成,设花园的BC边长为x(m),花园的面积为S(m2).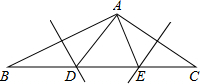 如图,在△ABC中,已知AB,AC的垂直平分线分别交BC于点D,E,且∠BAC=125°,则∠DAE是70度.
如图,在△ABC中,已知AB,AC的垂直平分线分别交BC于点D,E,且∠BAC=125°,则∠DAE是70度.