题目内容
14. 如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想:
如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想:(1)△BCG与△ACH全等吗?若全等,请说明理由.
(2)M、N分别是BE、AD的中点.
①△BCM≌△CAN吗?
②△CMN是等边三角形吗?
分析 (1)△BCG与△ACH全等,先根据等边三角形的性质可得AC=BC,CD=CE,∠ACB=∠DCE=60°,然后求出∠ACD=∠BCE,再利用“边角边”证明△ACD和△BCE全等,根据全等三角形对应角相等得到∠EBC=∠CAD,再证明∠ACB=∠ACH=60°,又BC=AC,可证得△BCG与△ACH全等;
(2)①△BCM≌△CAN,根据△ACD和△BCE全等,由全等三角形对应角相等得到∠EBC=∠CAD,BE=AD,由M、N分别是BE、AD的中点,可得BM=AN,即可证明△BCM≌△CAN;
②根据全等三角形对应角相等可得∠CAD=∠CBE,再根据中点定义求出AM=BN,然后利用“边角边”证明△ACM和△BCN全等,根据全等三角形对应边相等可得CM=CN,全等三角形对应角相等可得∠ACM=∠BCN,然后求出∠MCN=∠ACB=60°,从而得证.
解答 解:(1)△BCG与△ACH全等,
∵△ABC、△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACB+∠BCD=∠ACD,
∠DCE+∠BCD=∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠EBC,
∵∠ACB=∠DCE=60°,
∴∠ACH=180°-∠ACB-∠DCE=60°,
∴∠ACB=∠ACH,
在△BCG和△ACH中,
$\left\{\begin{array}{l}{∠GBC=∠CAH}\\{BC=AC}\\{∠GCB=∠ACH}\end{array}\right.$,
∴△BCG≌△ACH.
(2)①△BCM≌△CAN,
∵△ACD≌△BCE,
∴∠EBC=∠CAD,BE=AD,
∵M、N分别是BE、AD的中点,
∴BM=AN,
在△BCM和△CAN中,
$\left\{\begin{array}{l}{BC=AC}\\{∠MBC=∠NAC}\\{BM=AN}\end{array}\right.$,
∴△BCM≌△CAN(SAS).
②△MNC是等边三角形.
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵点M、N分别是线段AD、BE的中点,AD=BE,
∴AM=BN,
在△ACM和△BCN中,
$\left\{\begin{array}{l}{AC=BC}\\{∠CAD=∠CBE}\\{AM=BN}\end{array}\right.$,
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
∴∠MCN=∠BCM+∠BCN=∠BCM+∠ACM=∠ACB=60°,
∴△MNC是等边三角形.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质与判定,熟练掌握三角形全等的判定方法并准确识图找出全等的条件是解题的关键.

(1)列表:
| x | … | -3 | 0 | 1 | 2 | … | |||
| y=-x2 | … | -4 | -1 | -9 | … |
(3)函数y=-x2的图象是一条抛物线,开口向下,对称轴为y(x或y)轴,顶点坐标是(0,0),函数有最大(大或小)值0.
(4)在函数y=-x2中,当x>0时,若x1>x2,函数值y1<y2;当x<0时,若x1>x2,函数值y1>y2.
 如图,一个长为5m的梯子斜靠在墙上,梯子的底端距墙4m.
如图,一个长为5m的梯子斜靠在墙上,梯子的底端距墙4m. 如图,某居民小区要在一块一边靠墙(墙长20m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为50m的栅栏围成,设花园的BC边长为x(m),花园的面积为S(m2).
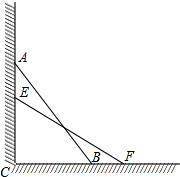
如图,某居民小区要在一块一边靠墙(墙长20m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为50m的栅栏围成,设花园的BC边长为x(m),花园的面积为S(m2). 如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.
如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.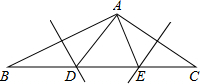 如图,在△ABC中,已知AB,AC的垂直平分线分别交BC于点D,E,且∠BAC=125°,则∠DAE是70度.
如图,在△ABC中,已知AB,AC的垂直平分线分别交BC于点D,E,且∠BAC=125°,则∠DAE是70度.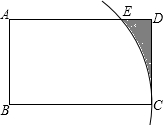 如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.
如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.