题目内容
 如图,在四边形ABCD中,DE∥BC,BD=CD,∠BCE=90°,以BD为直径的⊙O交CE于F、G,交BC于M.
如图,在四边形ABCD中,DE∥BC,BD=CD,∠BCE=90°,以BD为直径的⊙O交CE于F、G,交BC于M.(1)求证:BC=2DE;(2)求证:EF=CG.
考点:全等三角形的判定与性质,圆周角定理
专题:
分析:(1)连接DM,由等腰三角形的性质可得BM=CM,再证明四边形DECM是矩形可得DE=CM,进而证明BC=2DE;
(2)连接DF,GM,证明△RtDEF≌Rt△MCG即可得到EF=CG.
(2)连接DF,GM,证明△RtDEF≌Rt△MCG即可得到EF=CG.
解答:证明:(1)连接DM,
∵BD为⊙O的直径,
∴∠DMC=90°,
∴DM⊥BC,
∵BD=CD,
∴BM=CM,
∵∠BCE=90°,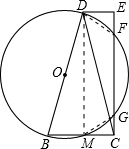
∴DM∥CE,
∵DE∥BC,
∴四边形DECM是矩形,
∴DE=CM;
∴BC=2DE;
(2)连接DF,GM,
∵DM∥EC,
∴∠MDC=∠DCE,
∴MG=DF,
∵四边形DECM是矩形,
∴DE=CM,∠DEF=∠MCG=90°,
在△RtDEF和Rt△MCG中,
,
∴△RtDEF≌Rt△MCG(HL),
∴EF=CG.
∵BD为⊙O的直径,
∴∠DMC=90°,
∴DM⊥BC,
∵BD=CD,
∴BM=CM,
∵∠BCE=90°,

∴DM∥CE,
∵DE∥BC,
∴四边形DECM是矩形,
∴DE=CM;
∴BC=2DE;
(2)连接DF,GM,
∵DM∥EC,
∴∠MDC=∠DCE,
∴MG=DF,
∵四边形DECM是矩形,
∴DE=CM,∠DEF=∠MCG=90°,
在△RtDEF和Rt△MCG中,
|
∴△RtDEF≌Rt△MCG(HL),
∴EF=CG.
点评:本题考查了全等三角形的判定和性质,圆周角定理,平行线的性质,等腰三角形的性质以及矩形的判定和性质,同时也考查了学生的推理证明的能力.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
在实数0、3、-
、2.236、π、3.14中无理数的个数是( )
| 6 |
| A、1 | B、2 | C、3 | D、4 |
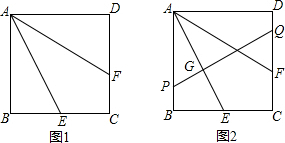
 如图所示,已知AB⊥BC,DC⊥BC,E在BC上,且AE=AD,AB=BC,求证:CE=CD.
如图所示,已知AB⊥BC,DC⊥BC,E在BC上,且AE=AD,AB=BC,求证:CE=CD.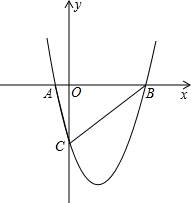 如图,在△ABC中,点A在x轴负半轴上,点B在x轴正半轴上,AB=6,点C在y轴负半轴上,且OC=5,抛物线y=a(x-2)2+k经过△ABC的三个顶点.
如图,在△ABC中,点A在x轴负半轴上,点B在x轴正半轴上,AB=6,点C在y轴负半轴上,且OC=5,抛物线y=a(x-2)2+k经过△ABC的三个顶点. 在平面直角坐标系xOy中,抛物线y=x2-(m-1)x-m(m>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=x2-(m-1)x-m(m>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C. 如图所示,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于F,求证:BP=2PF.
如图所示,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于F,求证:BP=2PF.