题目内容
 如图所示,已知AB⊥BC,DC⊥BC,E在BC上,且AE=AD,AB=BC,求证:CE=CD.
如图所示,已知AB⊥BC,DC⊥BC,E在BC上,且AE=AD,AB=BC,求证:CE=CD.考点:全等三角形的判定与性质
专题:证明题
分析:过点A作BC的平行线交CD的延长线于F,易证Rt△ABE≌Rt△AFD,所以∠AEB=∠ADF,AE=AD,进而可得∠AED=∠ADE,所以∠DEC=∠EDC,由等角对等边可得CE=CD.
解答:证明:过点A作BC的平行线交CD的延长线于F,
∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,
∴AB∥CF,
∵AB=BC,
∴四边形ABCF是正方形,
∴AF=AB,
在Rt△ABE和Rt△AFD中,
∴Rt△ABE≌Rt△AFD,
∴∠AEB=∠ADF,AE=AD,
∴∠AED=∠ADE,
∴∠CED=∠CDE,
∴DC=CE.

∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,
∴AB∥CF,
∵AB=BC,
∴四边形ABCF是正方形,
∴AF=AB,
在Rt△ABE和Rt△AFD中,
|
∴Rt△ABE≌Rt△AFD,
∴∠AEB=∠ADF,AE=AD,
∴∠AED=∠ADE,
∴∠CED=∠CDE,
∴DC=CE.
点评:本题考查了正方形的判定和性质、全等三角形的判定和性质以及等腰三角形的判定和性质,题目的综合性较强,解题的关键是添加辅助线,构造全等三角形.

练习册系列答案
相关题目
钦州市近年开发的“八寨沟”旅游风景区气候宜人,环境空气质量达到I类标准.空气中的可吸入微粒物年平均浓度只有0.000 0238g/m3,用科学记数法表示为( )g/m3.
| A、0.238×107 |
| B、2.38×10-7 |
| C、23.8×10-6 |
| D、2.38×10-5 |
温度上升记为正,-2℃表示的意义是( )
| A、下降2℃ | B、负2℃ |
| C、零下2℃ | D、下降-2℃ |
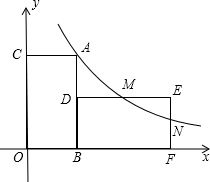 如图,面积为8的矩形ABOC的边OB,OC分别在x轴,y轴的正半轴上,点A在反比例函数y=
如图,面积为8的矩形ABOC的边OB,OC分别在x轴,y轴的正半轴上,点A在反比例函数y= 如图,△ABC中,∠BAC的平分线AD交BC的中垂线DE于D,E为垂足,过D作DM⊥AB于M,DN⊥AC交AC的延长线于N,求证:BM=CN.
如图,△ABC中,∠BAC的平分线AD交BC的中垂线DE于D,E为垂足,过D作DM⊥AB于M,DN⊥AC交AC的延长线于N,求证:BM=CN.
 如图,在四边形ABCD中,DE∥BC,BD=CD,∠BCE=90°,以BD为直径的⊙O交CE于F、G,交BC于M.
如图,在四边形ABCD中,DE∥BC,BD=CD,∠BCE=90°,以BD为直径的⊙O交CE于F、G,交BC于M.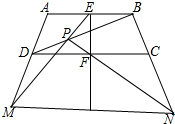 如图,已知四边形ABCD,E是AB中点,F是CD中点,P是BD对角线上一点,EP延长线交AD延长线于点M,PF延长线交BC延长线于点N,证明:直线EF平分MN.
如图,已知四边形ABCD,E是AB中点,F是CD中点,P是BD对角线上一点,EP延长线交AD延长线于点M,PF延长线交BC延长线于点N,证明:直线EF平分MN.