题目内容
 如图所示,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于F,求证:BP=2PF.
如图所示,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于F,求证:BP=2PF.考点:全等三角形的判定与性质,等边三角形的性质,含30度角的直角三角形
专题:证明题
分析:首先证△ABD≌△CAE,推出∠ABD=∠CAE,求出∠BPF=∠APD=60°,得出∠PBF=30°,根据含30度角的直角三角形性质求出即可.
解答:解:∵△ABC是等边三角形,
∴AB=AC,
∠BAC=∠C,
在△ABD和△CAE中,
,
∴△ABD≌△CAE,
∴∠ABD=∠CAE,
∴∠APD=∠ABP+∠PAB=∠BAC=60°,
∴∠BPF=∠APD=60°,
在Rt△BFP中,∠PBF=30°,
∴BP=2PF,
∴AB=AC,
∠BAC=∠C,
在△ABD和△CAE中,
|
∴△ABD≌△CAE,
∴∠ABD=∠CAE,
∴∠APD=∠ABP+∠PAB=∠BAC=60°,
∴∠BPF=∠APD=60°,
在Rt△BFP中,∠PBF=30°,
∴BP=2PF,
点评:本题考查了等边三角形性质,全等三角形的性质和判定,三角形外角性质,含30度角的直角三角形性质的应用,关键是求出∠PBF=30°.

练习册系列答案
相关题目
若∠A=41°,则cosA的大致范围是( )
| A、0<cosA<1 | ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,△ABC中,∠BAC的平分线AD交BC的中垂线DE于D,E为垂足,过D作DM⊥AB于M,DN⊥AC交AC的延长线于N,求证:BM=CN.
如图,△ABC中,∠BAC的平分线AD交BC的中垂线DE于D,E为垂足,过D作DM⊥AB于M,DN⊥AC交AC的延长线于N,求证:BM=CN. 如图,在四边形ABCD中,DE∥BC,BD=CD,∠BCE=90°,以BD为直径的⊙O交CE于F、G,交BC于M.
如图,在四边形ABCD中,DE∥BC,BD=CD,∠BCE=90°,以BD为直径的⊙O交CE于F、G,交BC于M.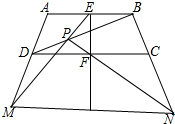 如图,已知四边形ABCD,E是AB中点,F是CD中点,P是BD对角线上一点,EP延长线交AD延长线于点M,PF延长线交BC延长线于点N,证明:直线EF平分MN.
如图,已知四边形ABCD,E是AB中点,F是CD中点,P是BD对角线上一点,EP延长线交AD延长线于点M,PF延长线交BC延长线于点N,证明:直线EF平分MN. 要把由5个小正方形组成的十字形纸板(如图)剪开,使剪成的若干块能够拼成一个大正方形.
要把由5个小正方形组成的十字形纸板(如图)剪开,使剪成的若干块能够拼成一个大正方形.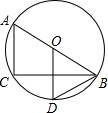 如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交于点D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交于点D.