题目内容
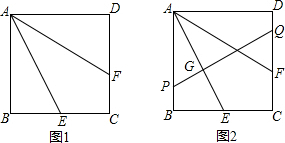
如图1:在正方形ABCD中,E是BC的中点,点F在CD上,∠BAE=∠FAE.
(1)指出线段AF、BC、FC之间有什么关系,证明你的结论.
(2)设AB=12,求线段FC的长.
(3)如图2:过AE中点G的直线分别交AB、CD于P、Q;求
的值.
(1)指出线段AF、BC、FC之间有什么关系,证明你的结论.
(2)设AB=12,求线段FC的长.
(3)如图2:过AE中点G的直线分别交AB、CD于P、Q;求
| PG |
| QG |

考点:四边形综合题
专题:
分析:(1)过E作EM⊥AF交AF于点M,则可证明△ABE≌△AME,△EMF≌△ECF,可得出结论;
(2)设FC=x,借助(1)的结论可得出AF=12+x,DF=12-x,在Rt△ADF中由勾股定理得出方程求解即可;
(3)过G作BC的平行线RS,由条件可得出RG=
BC,SG=
BC,再由平行线分线段成比例可求出
的值.
(2)设FC=x,借助(1)的结论可得出AF=12+x,DF=12-x,在Rt△ADF中由勾股定理得出方程求解即可;
(3)过G作BC的平行线RS,由条件可得出RG=
| 1 |
| 4 |
| 3 |
| 4 |
| PG |
| QG |
解答:解:(1)AF=BC+FC,证明如下:
如图1,过E作EM⊥AF交AF于点M,

∵∠BAE=∠FAE,
∴BE=ME,
在Rt△ABE和Rt△AME中,
,
∴Rt△ABE≌Rt△AME(HL),
∴AM=AB=BC,ME=BE=EC,
在Rt△MFE和Rt△CFE中,
,
∴Rt△MFE≌Rt△CFE(HL),
∴MF=FC,
∴AF=AM+MF=BC+FC;
(2)设FC=x,由(1)可知MF=x,AM=AD=AB=12,则DF=12-x,AF=12+x,
在Rt△AFD中,由勾股定理可得:AD2+DF2=AF2,
即122+(12-x)2=(12+x)2,解得x=3,
即FC=3;
(3)如图2,过G作RS∥BC,交AB于点R,交CD于点S,

∵G为AE中点,
∴R为AB中点,
∴RG=
BE=
BC,GS=RS-RG=BC-RG=BC-
BC=
BC,
∵AB∥CD,
∴
=
=
=
.
如图1,过E作EM⊥AF交AF于点M,

∵∠BAE=∠FAE,
∴BE=ME,
在Rt△ABE和Rt△AME中,
|
∴Rt△ABE≌Rt△AME(HL),
∴AM=AB=BC,ME=BE=EC,
在Rt△MFE和Rt△CFE中,
|
∴Rt△MFE≌Rt△CFE(HL),
∴MF=FC,
∴AF=AM+MF=BC+FC;
(2)设FC=x,由(1)可知MF=x,AM=AD=AB=12,则DF=12-x,AF=12+x,
在Rt△AFD中,由勾股定理可得:AD2+DF2=AF2,
即122+(12-x)2=(12+x)2,解得x=3,
即FC=3;
(3)如图2,过G作RS∥BC,交AB于点R,交CD于点S,

∵G为AE中点,
∴R为AB中点,
∴RG=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
∵AB∥CD,
∴
| PG |
| QG |
| RG |
| SG |
| ||
|
| 1 |
| 3 |
点评:本题主要考查正方形的性质及全等三角形的判定和性质、平行线分线段成比例定理的综合应用,在(1)中构造三角形全等找到线段之间的关系是解题的关键,在(3)中过G作平行线把
的值转化成
是解题的关键.
| PG |
| QG |
| RG |
| SG |

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
钦州市近年开发的“八寨沟”旅游风景区气候宜人,环境空气质量达到I类标准.空气中的可吸入微粒物年平均浓度只有0.000 0238g/m3,用科学记数法表示为( )g/m3.
| A、0.238×107 |
| B、2.38×10-7 |
| C、23.8×10-6 |
| D、2.38×10-5 |
 如图,已知AB为弦,MC为切线,BM⊥AB,求证:AC∥DM.
如图,已知AB为弦,MC为切线,BM⊥AB,求证:AC∥DM.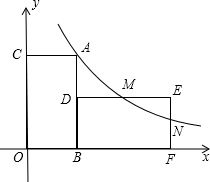 如图,面积为8的矩形ABOC的边OB,OC分别在x轴,y轴的正半轴上,点A在反比例函数y=
如图,面积为8的矩形ABOC的边OB,OC分别在x轴,y轴的正半轴上,点A在反比例函数y= 如图,△ABC中,∠BAC的平分线AD交BC的中垂线DE于D,E为垂足,过D作DM⊥AB于M,DN⊥AC交AC的延长线于N,求证:BM=CN.
如图,△ABC中,∠BAC的平分线AD交BC的中垂线DE于D,E为垂足,过D作DM⊥AB于M,DN⊥AC交AC的延长线于N,求证:BM=CN. 如图,在四边形ABCD中,DE∥BC,BD=CD,∠BCE=90°,以BD为直径的⊙O交CE于F、G,交BC于M.
如图,在四边形ABCD中,DE∥BC,BD=CD,∠BCE=90°,以BD为直径的⊙O交CE于F、G,交BC于M.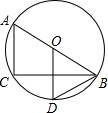 如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交于点D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交于点D.