题目内容
5.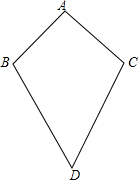 如图,在筝形四边形ABDC中,AB=AC,BD=CD,已知∠BAC=80°,∠BDC=60°,试求∠B的大小.
如图,在筝形四边形ABDC中,AB=AC,BD=CD,已知∠BAC=80°,∠BDC=60°,试求∠B的大小.
分析 连接AD,利用“SSS”证得△ABD≌△ACD,得出∠BAD=∠CAD,∠BDA=∠CDA,进一步利用三角形的内角和定理求得答案即可.
解答 解:如图,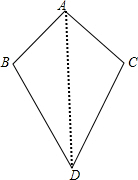
连接AD,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{BD=BC}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD,
∴∠BAD=∠CAD,∠BDA=∠CDA,
∵∠BAC=80°,∠BDC=60°,
∴∠BAD=40°,∠BDA=30°,
∴∠B=180°-∠BAD-∠BDA=110°.
点评 此题考查全等三角形的判定与性质,三角形的内角和定理,掌握三角形全等的判定方法是解决问题的关键.

练习册系列答案
相关题目
17.某校篮球队10名队员的身高(精确到cm)如表所示,则10名队员身高的众数是172cm.
| 身高(单位:cm) | 163 | 165 | 168 | 172 | 175 |
| 人 数 | 1 | 2 | 2 | 3 | 2 |
14.在△ABC中,BC=a,AB=c,CA=b.且a、b、c满足:a2-8b=-23,b2-10c=-34,c2-6a=7,则2sinA+sinB=( )
| A. | 1 | B. | $\frac{7}{5}$ | C. | 2 | D. | $\frac{12}{5}$ |
15.一元二次方程3x2=x的解是( )
| A. | x=0 | B. | x1=0,x2=3 | C. | x1=0,x2=$\frac{1}{3}$ | D. | x=$\frac{1}{3}$ |
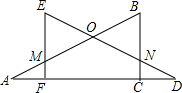 两块含30°角的全等直角三角形木板,按如图所示方式摆放,使得两条相等的直角边AC,DF在同一条直线上.此时MF与NC是否相等?请说明理由.
两块含30°角的全等直角三角形木板,按如图所示方式摆放,使得两条相等的直角边AC,DF在同一条直线上.此时MF与NC是否相等?请说明理由.