题目内容
14.在△ABC中,BC=a,AB=c,CA=b.且a、b、c满足:a2-8b=-23,b2-10c=-34,c2-6a=7,则2sinA+sinB=( )| A. | 1 | B. | $\frac{7}{5}$ | C. | 2 | D. | $\frac{12}{5}$ |
分析 利用完全平方公式把这个式子写成平方几个非负数的和的形式,求得a,b,c的值,进而判断出三角形的形状即可.再运用三角函数定义求解即可.
解答 解:∵a2-8b=-23,b2-10c=-34,c2-6a=7,
∴a2-8b+b2-10c+c2-6a=-50,
∴a2-6a+9+b2-8b+16+c2-10c+25=0,
∴(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∴这个三角形的形状是直角三角形,
∴2sinA+sinB=2,
故选C.
点评 本题考查完全平方公式和勾股定理的逆定理在实际中的运用,注意运用几个非负数的和为0,那么这几个数均为0这个知识点是解题关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
4.下列方程是一元二次方程的是( )
| A. | (x-3)2=(x+5)2 | B. | $\frac{1}{{x}^{2}+1}$=4 | C. | x2=4 | D. | ax2+bx+c=0 |
 如图,在△ABC中,∠ABC=48°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,则∠ADC=66°.
如图,在△ABC中,∠ABC=48°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,则∠ADC=66°.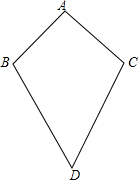 如图,在筝形四边形ABDC中,AB=AC,BD=CD,已知∠BAC=80°,∠BDC=60°,试求∠B的大小.
如图,在筝形四边形ABDC中,AB=AC,BD=CD,已知∠BAC=80°,∠BDC=60°,试求∠B的大小.