题目内容
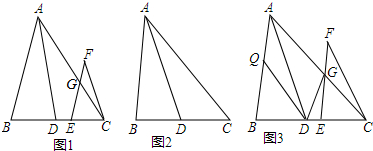
1.在△ABC中,AD平分∠BAC,点E在射线DC上,EF∥AB,CF∥AD,EF与射线AC交于点G,(1)当点E在线段DC上时(如图1),求证:∠EGC=2∠GFC;
(2)当点E在线段DC的延长线上时,在图2补全图形,并写出∠EGC与∠GFC的数量关系;
(3)在(1)的条件下,连接GD,过点D作DQ⊥DG,交AB于点Q(如图3),当∠BAC=90°,应满足∠GFC=2∠DGE时,探究∠BQD与∠DGE的数量关系,并加以证明.
分析 (1)根据平行线的性质证明∠EGC=∠BAC,∠EFC=∠BAD,然后利用角平分线的定义证明;
(2)首先利用平行线的性质证明∠DAC=∠FCG,∠BAC=∠EGC,然后利用三角形的外角等于不相邻的两个内角的和,即可证明∠EGC=2∠DAC,从而证得;
(3)首先证明A、G、D、Q四点共圆,然后根据圆周角定理以及平行线的性质证得.
解答 (1)证明:∵EF∥AB,
∴∠EGC=∠BAC,
又∵CF∥AD,
∴∠EFC=∠BAD,
又∵AD平分∠BAD,即∠BAD=$\frac{1}{2}$∠BAC,
∴∠EGC=2∠GFC;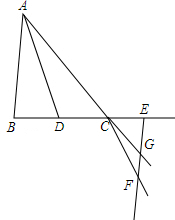
(2)∠EGC=2∠EFC.理由是:解:∵AD∥CF,
∴∠DAC=∠FCG,
∵AB∥EF,
∴∠BAC=∠EGC,
又∵AD平分∠BAC,即∠DAC=$\frac{1}{2}$∠BAC,
∴∠EGC=2∠DAC,
又∵∠EGC=∠GCF+∠GFC,
∴∠EGC=2∠EFC;
(3)∵∠BAC=90°,∠QDG=90°,
∴A、G、D、Q四点共圆.
∴∠BQD=∠AGD,
又∵EF∥AB,
∴∠AGE=90°,
∴∠AGD+∠DGE=90°,
∴∠BQD+∠DGE=90°,
又∵∠EGC=2∠GFC=4∠DGE=90°,
∴∠DGE=22.5°,
∴∠BQD=67.5°,
∴∠BQD=3∠DGE.
点评 本题考查了平行线的性质以及四点共共圆和圆周角定理,注意到A、G、D、Q四点共圆是解题的关键.

练习册系列答案
相关题目
11.方程x2-3x+$\sqrt{3}$=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实根 | D. | 没有实数根 |
10.已知⊙O的直径为4,点P到点O的距离为3,则下列对于点P与⊙O位置关系的说法正确的是( )
| A. | 在圆上 | B. | 在圆内 | C. | 在圆外 | D. | 不确定 |
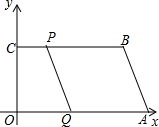 已知,点A(10,0),C(0,3),B(6,3),动点P、Q分别从C、A两点同时出发,点P以每秒1个单位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5).
已知,点A(10,0),C(0,3),B(6,3),动点P、Q分别从C、A两点同时出发,点P以每秒1个单位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5).