题目内容
11.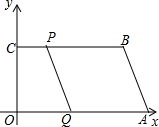 已知,点A(10,0),C(0,3),B(6,3),动点P、Q分别从C、A两点同时出发,点P以每秒1个单位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5).
已知,点A(10,0),C(0,3),B(6,3),动点P、Q分别从C、A两点同时出发,点P以每秒1个单位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5).(1)求点P和点Q的坐标(用“t”表示);
(2)当t为多少时,BP=AQ?
(3)当t为多少时,PQ=AB?
分析 (1)根据B、C的纵坐标相同,可知BC∥OA,根据题意得CP=t,AQ=2t,则OQ=10-2t,即可得出P、Q点的坐标;
(2)当BP=AQ时,利用Q(10-2t,0)P(t,3)推出 6-t=10-2t,从而可求出t.
(2)当PQ=AB时,四边形PQAB为等腰梯形,根据勾股定理求出AB=5,再利用等腰梯形的性质可得9t2-60t+109=25,解得t即可.
解答 解:(1)∵C(0,3),B(6,3),
∴BC∥OA,
由题意可知:CP=t,AQ=2t,
∴OQ=10-2t,
∴P(t,3),Q(10-2t,0);
(2)∵BP‖AQ,BP=AQ,
∴PQAB为平行四边形时,
∵BP=6-t,AQ=2t
∴6-t=2t
解得t=2,
∴当t=2时,BP=AQ;
(3)∵BP‖AQ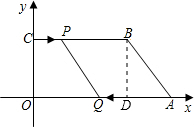 ,QP=AB
,QP=AB
∴四边形PQAB为等腰梯形.
如图,过点B作BD⊥OA于点D,
∵A点坐标为(10,0),B点坐标为(6,3).
∴DA=4,BD=3,
∴在直角△ABD中,由勾股定理知AB=$\sqrt{{4}^{2}+{3}^{2}}$=5,
PQ=$\sqrt{(10-2t-t)^{2}+(3-0)^{2}}$,
∵AB=PQ,
∴9t2-60t+109=25
9t2-60t+84=0
3t2-20t+28=0
(3t-14)(t-2)=0
解得t1=$\frac{14}{3}$,t2=2
又∵t=2时PQAB为平行四边形 ( (1)中已证 )
所以t=$\frac{14}{3}$.
点评 此题是四边形的综合题,主要考查等腰梯形的性质,平行四边形的性质及点的坐标等知识点.掌握平行四边形的对边平行且相等,等腰梯形两腰相等是解题的关键.化“动为静”是解决运动类问题的基本思路,即用t表示出线段的长度,从而得到关于t的方程求解.注意掌握数形结合思想与方程思想的应用.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案(1)有理数的绝对值一定比0大;
(2)有理数的相反数一定比0小;
(3)如果两个数的绝对值相等,那么这两个数相等;
(4)互为相反数的两个数的绝对值相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | (x+3)2=8 | B. | (x-3)2=8 | C. | (x-3)2=10 | D. | (x+3)2=10 |
 如图,将△ABC绕点C顺时针方向旋转50°得到△A′CB′,若AC⊥A′B′,则∠BAC=40°.
如图,将△ABC绕点C顺时针方向旋转50°得到△A′CB′,若AC⊥A′B′,则∠BAC=40°.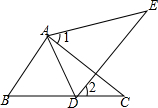 如图,点D在BC上,∠1=∠2,AE=AC,下面三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并证明两三角形全等.
如图,点D在BC上,∠1=∠2,AE=AC,下面三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并证明两三角形全等.