题目内容
20.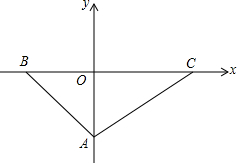 如图,已知在平面直角坐标系中,点A在y轴上,点B、C在x轴上,S△ABO=8,OA=OB,BC=10,点P的坐标是(-6,a),
如图,已知在平面直角坐标系中,点A在y轴上,点B、C在x轴上,S△ABO=8,OA=OB,BC=10,点P的坐标是(-6,a),(1)求△ABC三个顶点A、B、C的坐标;
(2)连接PA、PB,并用含字母a的式子表示△PAB的面积(a≠2);
(3)在(2)问的条件下,是否存在点P,使△PAB的面积等于△ABC的面积?如果存在,请求出点P的坐标;若不存在,请说明理由.
分析 (1)根据三角形面积公式得到$\frac{1}{2}$•OA2=8,解得OA=4,则OB=OA=4,OC=BC-OB=6,然后根据坐标轴上点的坐标特征写出△ABC三个顶点的坐标;
(2)分类讨论:当点P在在直线AB上方即a>2;当点P在直线AB下方,即a<2;利用面积的和与差求解;
(3)先计算出S△ABC=20,利用(2)中的结果得到方程,然后分别求出a的值,从而确定P点坐标.
解答 解:(1)∵S△ABO=$\frac{1}{2}$OA•OB,
∵OA=OB,
∴$\frac{1}{2}$OA2=8,解得OA=4,
∴OB=OA=4,
∴OC=BC-OB=10-4=6,
∴A(0,-4),B(-4,0),C(6,0);
(2)当点P在第二象限,直线AB的上方,即a>2,作PH⊥y轴于H,如图,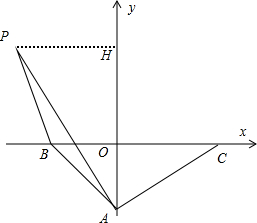
S△PAB=S△AOB+S梯形BOHP-S△PBH=8+$\frac{1}{2}$(4+6)•a-$\frac{1}{2}$•6•(a+4)=2a-4;
当点P在直线AB下方,即a<2,作PH⊥x轴于H,如图,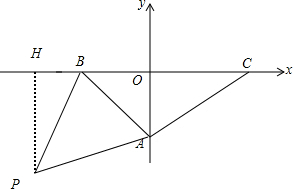
S△PAB=S梯形OHPA-S△PBH-S△OAB=$\frac{1}{2}$(-a+4)•6-$\frac{1}{2}$•(6-4)•(-a)-8=4-2a;
(3)S△ABC=$\frac{1}{2}$×10×4=20,
当2a-4=20,
解得a=12.
此时P点坐标为(-6,12);
当4-2a=20,
解得a=-8.
此时P点坐标为(-6,-8).
综上所述,点P的坐标为(-6,12)或(-6,-8).
点评 本题考查了坐标与图形性质,利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系;掌握三角形面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE,求证:BC=AE.
已知:D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE,求证:BC=AE.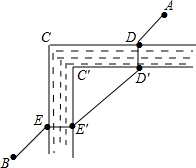 如图,荆州护城河同在CC′处直角转弯,同宽均为5米,从A处到达B处,须经过两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西,南北方向的,如何架桥可使ADD′E′EB的路程最短?
如图,荆州护城河同在CC′处直角转弯,同宽均为5米,从A处到达B处,须经过两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西,南北方向的,如何架桥可使ADD′E′EB的路程最短?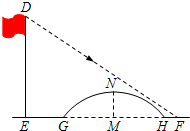 如图,某小组开展了测算小桥所在圆的半径的活动,测得EF的长为12m,EG的长为3m,HF的长为1m,测得拱高($\widehat{GH}$的中点N到弦GH的距离,即MN的长)为2m.请你帮助计算小桥所在圆的半径.
如图,某小组开展了测算小桥所在圆的半径的活动,测得EF的长为12m,EG的长为3m,HF的长为1m,测得拱高($\widehat{GH}$的中点N到弦GH的距离,即MN的长)为2m.请你帮助计算小桥所在圆的半径. 如图.已知△ABC≌△DCB,AB=CD,∠1=∠2,求证:AD∥BC.
如图.已知△ABC≌△DCB,AB=CD,∠1=∠2,求证:AD∥BC.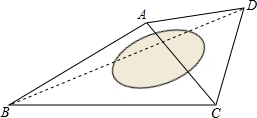 某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=60°,试求水池两旁B,D两点之间的距离.
某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=60°,试求水池两旁B,D两点之间的距离.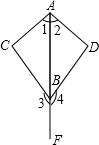 如图,∠3、∠4分别为△ABC与△ABD的外角.已知∠1=∠2,∠3=∠4.求证:AC=AD.
如图,∠3、∠4分别为△ABC与△ABD的外角.已知∠1=∠2,∠3=∠4.求证:AC=AD.