题目内容
12.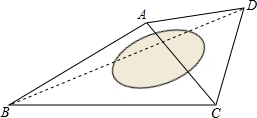 某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=60°,试求水池两旁B,D两点之间的距离.
某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=60°,试求水池两旁B,D两点之间的距离.
分析 以AB为边在△ABC外侧作等边△ABE,连接CE,求出△EAC≌△DAB可得:BD=CE,证明△EBC是直角三角形,利用勾股定理求出CE的长度,即可解答.
解答  解:以AB为边在△ABC外侧作等边△ABE,连接CE.
解:以AB为边在△ABC外侧作等边△ABE,连接CE.
∵∠EAB=∠DAC=60°,
∴∠EAB+∠BAC=∠DAC+∠BAC,
∴∠EAC=∠DAB,
在△EAC和△DAB中,
$\left\{\begin{array}{l}{AE=AB}\\{∠EAC=∠DAB}\\{AC=AD}\end{array}\right.$,
∴△EAC≌△DAB(SAS),
∴BD=CE,
∴∠EBC=60°+30°=90°,
∴△EBC是直角三角形,
∵EB=60m BC=80m,
∴CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=$\sqrt{6{0}^{2}+8{0}^{2}}$=100(m).
∴水池两旁B、D两点之间的距离为100m.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质与判定,熟记性质与判定方法是解题的关键,难点在于(灵活运用)作出辅助线构造成等边三角形和直角三角形.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
16.下列方程是二元一次方程的是( )
| A. | 2x+y=2(x-3y)+3 | B. | x+xy=4 | C. | $\frac{1}{x}$+$\frac{1}{y}$=6 | D. | x=-y |
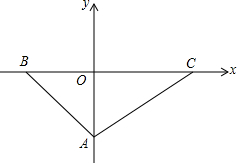 如图,已知在平面直角坐标系中,点A在y轴上,点B、C在x轴上,S△ABO=8,OA=OB,BC=10,点P的坐标是(-6,a),
如图,已知在平面直角坐标系中,点A在y轴上,点B、C在x轴上,S△ABO=8,OA=OB,BC=10,点P的坐标是(-6,a), 如图,已知一艘轮船有西向东航行,航行到A处测得小岛P的方向是北偏东75°,又航行10海里后.在B处测得小岛P的方向是北偏东60°,若小岛周围4.8海里内有暗礁.问:该轮船一直向东航行是否有触礁的危险!
如图,已知一艘轮船有西向东航行,航行到A处测得小岛P的方向是北偏东75°,又航行10海里后.在B处测得小岛P的方向是北偏东60°,若小岛周围4.8海里内有暗礁.问:该轮船一直向东航行是否有触礁的危险!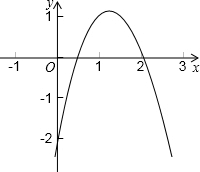 小明在阅读一本关于函数的课外读物时看到一段文字:“由图象知,当x=$\frac{5}{4}$时,二次函数y=■x2+5x-2有最大值”,则被墨迹污染的二次项系数是-2.
小明在阅读一本关于函数的课外读物时看到一段文字:“由图象知,当x=$\frac{5}{4}$时,二次函数y=■x2+5x-2有最大值”,则被墨迹污染的二次项系数是-2.