题目内容
3.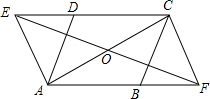 如图,在?ABCD中,OA=OC,EF过点O,点E、F分别在CD、AB的延长线上,求证:四边形AFCE是平行四边形.
如图,在?ABCD中,OA=OC,EF过点O,点E、F分别在CD、AB的延长线上,求证:四边形AFCE是平行四边形.
分析 由平行四边形的性质得出∠OCE=∠OAF,由ASA证明△OCE≌△OAF,得出对应边相等CE=AF,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠OCE=∠OAF,
在△OCE和△OAF中,$\left\{\begin{array}{l}{∠OCE=∠OAF}&{\;}\\{OC=OA}&{\;}\\{∠COE=∠AOF}&{\;}\end{array}\right.$,
∴△OCE≌△OAF(ASA),
∴CE=AF,
又∵CE∥AF,
∴四边形AFCE是平行四边形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目


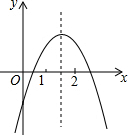 一次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;
一次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;