题目内容
15.如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)仔细观察,在图2中有3个以线段AC为边的“8字形”;
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP=$\frac{1}{3}$∠CAB,∠CDP=$\frac{1}{3}$∠CDB,试问∠P与∠C、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为360°.

分析 (1)以M为交点的“8字形”有1个,以O为交点的“8字形”有2个;
(2)根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C-∠P=∠P-∠B,即∠P=$\frac{1}{2}$(∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;
(3)与(2)的证明方法一样得到∠P=$\frac{1}{3}$(2∠C+∠B).
(4)根据三角形内角与外角的关系可得∠B+∠A=∠1,∠C+∠D=∠2,再根据四边形内角和为360°可得答案.
解答 解:(1)在图2中有3个以线段AC为边的“8字形”,
故答案为3;
(2)∵∠CAB和∠BDC的平分线AP和DP相交于点P,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C-∠P=∠P-∠B,
即∠P=$\frac{1}{2}$(∠C+∠B),
∵∠C=100°,∠B=96°
∴∠P=$\frac{1}{2}$(100°+96°)=98°;
(3)∠P=$\frac{1}{3}$(β+2α);
理由:∵∠CAP=$\frac{1}{3}$∠CAB,∠CDP=$\frac{1}{3}$∠CDB,
∴∠BAP=$\frac{2}{3}$∠BAC,∠BDP=$\frac{2}{3}$∠BDC,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C-∠P=$\frac{1}{3}$∠BDC-$\frac{1}{3}$∠BAC,∠P-∠B=$\frac{2}{3}$∠BDC-$\frac{2}{3}$∠BAC,
∴2(∠C-∠P)=∠P-∠B,
∴∠P=$\frac{1}{3}$(∠B+2∠C),
∵∠C=α,∠B=β,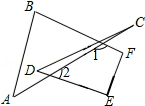
∴∠P=$\frac{1}{3}$(β+2α);
(4)∵∠B+∠A=∠1,∠C+∠D=∠2,
∴∠A+∠B+∠C+∠D=∠1+∠2,
∵∠1+∠2+∠F+∠E=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.
点评 本题考查了三角形内角与外角的关系,以及多边形内角和.也考查了角平分线的定义,关键是掌握三角形的外角等于与它不相邻的两个内角的和.

| A. | 4cm、6cm、8cm、10cm | B. | 4cm、6cm,8cm、12cm | ||
| C. | 11cm、22cm、33cm、66cm | D. | 2cm、4cm、4cm、8cm |
①线段;②等边三角形;③矩形;④菱形;⑤平行四边形.
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 2个 |
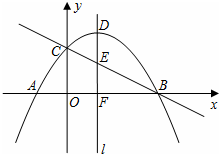 如图,抛物线y=-$\frac{1}{4}$x2+x+3与x轴相交于点A、B,与y轴相交于点C,顶点为点D,对称轴l与直线BC相交于点E,与x轴相交于点F.
如图,抛物线y=-$\frac{1}{4}$x2+x+3与x轴相交于点A、B,与y轴相交于点C,顶点为点D,对称轴l与直线BC相交于点E,与x轴相交于点F.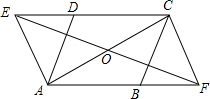 如图,在?ABCD中,OA=OC,EF过点O,点E、F分别在CD、AB的延长线上,求证:四边形AFCE是平行四边形.
如图,在?ABCD中,OA=OC,EF过点O,点E、F分别在CD、AB的延长线上,求证:四边形AFCE是平行四边形.