题目内容
19.下列分式中计算正确的是( )| A. | $\frac{2(y+z)}{x+3(y+z)}$=$\frac{2}{x+3}$ | B. | $\frac{x+y}{{x}^{2}+{y}^{2}}$=$\frac{2}{x+y}$ | ||
| C. | $\frac{(x-y)^{2}}{(y-x)^{2}}$=-1 | D. | $\frac{y-x}{2xy-{x}^{2}-{y}^{2}}$=$\frac{1}{x-y}$ |
分析 根据分式的基本性质,即可解答.
解答 解:A、分子与分母不能约去(y+z),故错误;
B、分子与分母不能约去(x+y),故错误;
C、$\frac{(x-y)^{2}}{(y-x)^{2}}$=1,故错误;
D、$\frac{y-x}{2xy-{x}^{2}-{y}^{2}}=\frac{-(x-y)}{-(x-y)^{2}}=\frac{1}{x-y}$,正确;
故选:D.
点评 本题考查了分式的基本性质,解决本题的关键是熟记分式的基本性质.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
14.下列图形和字母,是轴对称图形的是( )
①H ②E ③S ④ ⑤
⑤ ⑥
⑥
①H ②E ③S ④
 ⑤
⑤ ⑥
⑥
| A. | ①②③④⑤ | B. | ①②③ | C. | ①②⑤ | D. | ①②⑤⑥ |
4. 二次函数y=-x2+bx+c的大致图象如图所示,则下列结论不成立的是( )
二次函数y=-x2+bx+c的大致图象如图所示,则下列结论不成立的是( )
 二次函数y=-x2+bx+c的大致图象如图所示,则下列结论不成立的是( )
二次函数y=-x2+bx+c的大致图象如图所示,则下列结论不成立的是( )| A. | c=0 | B. | -1-b+c>0 | C. | -2<b<0 | D. | b>0 |
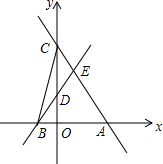 直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.
直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1. 如图,在Rt△ABC中,∠A=30°,点D是斜边AB的中点,点G是Rt△ABC的重心,GE⊥AC于点E.若BC=6cm,则GE=2cm.
如图,在Rt△ABC中,∠A=30°,点D是斜边AB的中点,点G是Rt△ABC的重心,GE⊥AC于点E.若BC=6cm,则GE=2cm. 如图,⊙C经过坐标原点O,并与两坐标轴分别交于A、D两点,已知∠OBA=30°,点A的坐标为(2,O).
如图,⊙C经过坐标原点O,并与两坐标轴分别交于A、D两点,已知∠OBA=30°,点A的坐标为(2,O). 已知矩形ABCD与圆心在AB上的⊙O相关于G、B、E、F点,并且CB=8,AG=1,DE=2,求CF的长度.
已知矩形ABCD与圆心在AB上的⊙O相关于G、B、E、F点,并且CB=8,AG=1,DE=2,求CF的长度.