题目内容
7.化简:$\root{3}{\frac{61}{125}-1}$=-$\frac{4}{5}$,$\sqrt{\frac{9}{64}}$=$\frac{3}{8}$,$\sqrt{(-9)^{2}}$=9.分析 先化简被开方数,然后依据立方根的定义求解即可;
依据算术平方根的定义求解即可;
先求得(-9)2,然后依据算术平方根的定义求解即可.
解答 解:$\root{3}{\frac{61}{125}-1}$=$\root{3}{-\frac{64}{125}}$=-$\frac{4}{5}$,$\sqrt{\frac{9}{64}}$=$\frac{3}{8}$,$\sqrt{(-9)^{2}}$=$\sqrt{81}$=9.
故答案为:$-\frac{4}{5}$;$\frac{3}{8}$;9.
点评 本题主要考查的是立方根、算术平方根的定义,熟练掌握相关定义是解题的关键.

练习册系列答案
相关题目
2.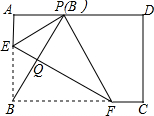 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )
如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )
 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )
如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )| A. | ①④ | B. | ①③ | C. | ②③ | D. | ①③④ |
12.下列四个条件中,不能判断四边形是平行四边形的条件是( )
| A. | 两组对边分别平行 | B. | 对角线互相平分 | ||
| C. | 两组对角分别相等 | D. | 一组对边平行,另一组对边相等 |
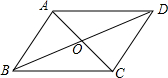 如图,在?ABCD中,已知AC、BD相交于点O,两条对角线的和为24cm,BC长为8cm,则△AOD的周长=20cm.
如图,在?ABCD中,已知AC、BD相交于点O,两条对角线的和为24cm,BC长为8cm,则△AOD的周长=20cm.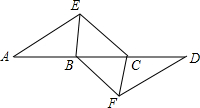 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC. 如图,在三角形ABC中,BE平分∠ABC,DE∥BC,则图中相等的角有5对.
如图,在三角形ABC中,BE平分∠ABC,DE∥BC,则图中相等的角有5对.