题目内容
2.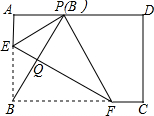 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )
如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )| A. | ①④ | B. | ①③ | C. | ②③ | D. | ①③④ |
分析 求出BE=2AE,根据翻折的性质可得PE=BE,再根据直角三角形30°角所对的直角边等于斜边的一半求出∠APE=30°,然后求出∠AEP=60°,再根据翻折的性质求出∠BEF=60°,根据直角三角形两锐角互余求出∠EFB=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半可得EF=2BE,判断出①正确;利用30°角的正切值求出PF=$\sqrt{3}$PE,判断出②错误;求出BE=2EQ,EF=2BE,然后求出FQ=3EQ,判断出③正确;求出∠PBF=∠PFB=60°,然后得到△PBF是等边三角形,进而得出2AP≠AB,故AD≠AB,即矩形ABCD不是正方形,判断出④错误.
解答 解:∵AE=$\frac{1}{3}$AB,
∴BE=2AE,
由翻折的性质得,PE=BE,
∴∠APE=30°,
∴∠AEP=90°-30°=60°,
∴∠BEF=$\frac{1}{2}$(180°-∠AEP)=$\frac{1}{2}$(180°-60°)=60°,
∴∠EFB=90°-60°=30°,
∴EF=2BE,故①正确;
∵BE=PE,
∴EF=2PE,
∵EF>PF,
∴PF<2PE,故②错误;
由翻折可知EF⊥PB,
∴∠EBQ=∠EFB=30°,
∴BE=2EQ,EF=2BE,
∴FQ=3EQ,故③正确;
由翻折的性质,∠EFB=∠EFP=30°,
则∠BFP=30°+30°=60°,
∵∠PBF=90°-∠EBQ=90°-30°=60°,
∴∠PBF=∠PFB=60°,
∴△PBF是等边三角形,
则$\sqrt{3}$AP=AB,
即2AP≠AB,故AD≠AB,
∴矩形ABCD不是正方形.
故④错误;
故选:B.
点评 本题考查了翻折变换的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,直角三角形两锐角互余的性质,等边三角形的判定等知识,熟记各性质并准确识图是解题的关键.

| A. | y=5x+1 | B. | y=5x+9 | C. | y=$\frac{1}{5}$x-$\frac{9}{5}$ | D. | y=$\frac{1}{5}$x+$\frac{1}{5}$ |
 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点). 如图,以?ABCD的一边为直径⊙O,恰好与边CD相切于点D,E是⊙O上一点,点E与点D位于直径AB的两侧.
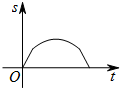
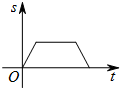
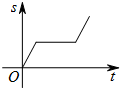
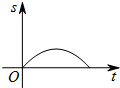
如图,以?ABCD的一边为直径⊙O,恰好与边CD相切于点D,E是⊙O上一点,点E与点D位于直径AB的两侧. 如图,一只蚂蚁从O点出发,在扇形AOB的边缘沿着O-A-B-O的路线匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
如图,一只蚂蚁从O点出发,在扇形AOB的边缘沿着O-A-B-O的路线匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )