题目内容
18.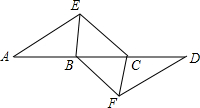 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.(1)求证:△AEC≌△DFB;
(2)若∠EBD=60°,BE=BC,求证四边形BFCE是菱形.
分析 (1)直接利用全等三角形的判定方法得出△ACE≌△DBF,即可得出答案;
(2)直接利用得出△EBC是等边三角形,进而利用菱形的判定方法得出答案.
解答 证明: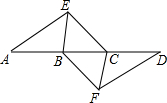 (1)∵AB=DC,
(1)∵AB=DC,
∴AB+BC=DC+BC,
即AC=DB,
在△ACE和△DBF中,
$\left\{\begin{array}{l}{AE=DB}\\{∠A=∠D}\\{AC=DB}\end{array}\right.$,
∴△ACE≌△DBF(SAS);
(2)∵△ACE≌△DBF,
∴EC=BF,∠ECA=∠FBD,
∴EC∥BF,
∴四边形BFCE是平行四边形,
∵∠EBD=60°,BE=BC,
∴△EBC是等边三角形,
∴EB=EC,
∴四边形BFCE是菱形.
点评 此题主要考查了全等三角形的判定与性质以及菱形的判定,正确掌握菱形的判定方法是解题关键.

练习册系列答案
相关题目

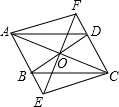 如图,在?ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC,EF与AB的延长线交于点E,与CD的延长线交于点F.
如图,在?ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC,EF与AB的延长线交于点E,与CD的延长线交于点F. 将矩形ABCD的一边AB沿AE对折,使AB沿AE对折,使AB落在边AD上,点B与点F重合,求证:四边形ABEF是正方形.
将矩形ABCD的一边AB沿AE对折,使AB沿AE对折,使AB落在边AD上,点B与点F重合,求证:四边形ABEF是正方形.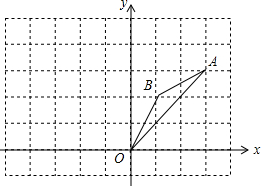 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,3),B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,3),B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).