题目内容
3.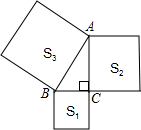 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )| A. | 15 | B. | 225 | C. | 81 | D. | 25 |
分析 根据正方形的面积公式求出BC、AB,根据勾股定理计算即可.
解答 解:∵S1=64,S3=289,
∴BC=8,AB=17,
由勾股定理得,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=15,
∴S2=152=225,
故选:B.
点评 本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
相关题目
18.$\sqrt{9}+\sqrt{16}$的值是( )
| A. | 7 | B. | -1 | C. | 1 | D. | -7 |
15.下列各数化简后与|3|相等的是( )
| A. | 3-1 | B. | (-1)3 | C. | |-3| | D. | -(-$\frac{1}{3}$) |
13.已知直线y=x+$\frac{3}{2}$与直线y=kx-1相交于点P,若点P的纵坐标为$\frac{1}{2}$,则关于x的不等式x+$\frac{3}{2}$>kx-1的解集为( )
| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |
 如图,A、C、F、B在同一直线上,AC=BF,AE=BD,且∠A=∠B.求证:EF∥CD.
如图,A、C、F、B在同一直线上,AC=BF,AE=BD,且∠A=∠B.求证:EF∥CD.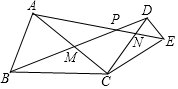 如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.
如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.



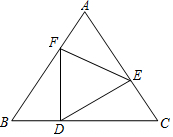 在△ABC中,己知AB=AC,点D、E、F分别在边BC、AC、AB上,且BD=CE,∠FDE=∠B,
在△ABC中,己知AB=AC,点D、E、F分别在边BC、AC、AB上,且BD=CE,∠FDE=∠B,