题目内容
12.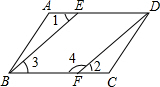 如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:
如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:解:因为AD∥BC(已知),所以∠1=∠3(已知).
因为∠1=∠2(已知),所以∠2=∠3.
所以BE∥DF (同位角相等,两直线平行).
所以∠3+∠4=180°(两直线平行,同旁内角互补).
分析 先根据平行线的性质得出∠1=∠3,再由∠1=∠2得出∠2=∠3,故可得出BE∥DF,据此可得出结论.
解答 解:因为AD∥BC(已知),
所以∠1=∠3(两直线平行,内错角相等).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥DF(同位角相等,两直线平行).
所以∠3+∠4=180°(两直线平行,同旁内角互补).
故答案为:已知;DF,同位角相等,两直线平行;两直线平行,同旁内角互补.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
3.在平面直角坐标系中,点(m2+1,1)一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.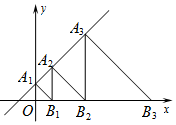 如图,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2017等于( )
如图,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2017等于( )
 如图,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2017等于( )
如图,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2017等于( )| A. | 24030 | B. | 24031 | C. | 24032 | D. | 24033 |
4.10-3等于( )
| A. | -30 | B. | -3 000 | C. | 0.001 | D. | -0.001 |
1.下列根式中能与$\sqrt{3}$合并的二次根式为( )
| A. | $\sqrt{\frac{3}{2}}$ | B. | $\sqrt{24}$ | C. | $\sqrt{12}$ | D. | $\sqrt{0.5}$ |
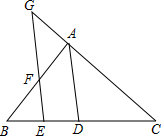 如图,在△ABC中,AD平分∠BAC,交BC于点D,点G在CA的延长线上,GE交AB,BC于点F,E,且∠BFE=∠G.
如图,在△ABC中,AD平分∠BAC,交BC于点D,点G在CA的延长线上,GE交AB,BC于点F,E,且∠BFE=∠G.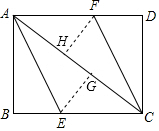 如图,在矩形ABCD中,AC是对角线,E、F分别在BC、AD边上,将边AB沿AE折叠,点B落在对角线AC上的G处,将边CD沿CF折叠,点D落在对角线AC上的点H处.
如图,在矩形ABCD中,AC是对角线,E、F分别在BC、AD边上,将边AB沿AE折叠,点B落在对角线AC上的G处,将边CD沿CF折叠,点D落在对角线AC上的点H处.
 如图,将一张长方形大铁皮切割成九块,切痕如图虚线所示,其中有两块是边长都为xdm的大正方形,两块是边长都为ydm的小正方形,五块是长宽分别是xdm、ydm的全等小长方形,且x>y.
如图,将一张长方形大铁皮切割成九块,切痕如图虚线所示,其中有两块是边长都为xdm的大正方形,两块是边长都为ydm的小正方形,五块是长宽分别是xdm、ydm的全等小长方形,且x>y.